What Is The Prime Factorization Of 192
Juapaving
Mar 27, 2025 · 5 min read
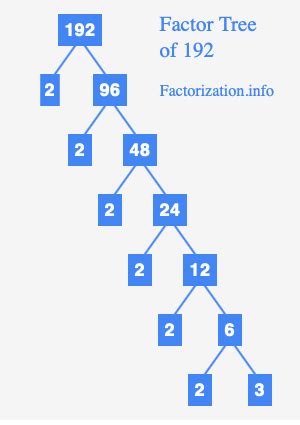
Table of Contents
What is the Prime Factorization of 192? A Deep Dive into Prime Numbers and Factorization
The seemingly simple question, "What is the prime factorization of 192?" opens a door to a fascinating world of number theory, prime numbers, and the fundamental building blocks of arithmetic. While the answer itself might be quickly obtained with a calculator or online tool, understanding the process of prime factorization is crucial for grasping core mathematical concepts and developing problem-solving skills applicable far beyond simple number decomposition. This article will not only provide the answer but also delve deeply into the concepts behind it, exploring different methods, applications, and the significance of prime factorization in various fields.
Understanding Prime Numbers
Before diving into the factorization of 192, let's establish a firm understanding of what constitutes a prime number. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. This means it's only divisible without a remainder by 1 and itself. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. Prime numbers are the fundamental building blocks of all other integers, as we'll see later.
Important Note: The number 1 is not considered a prime number, despite only being divisible by 1 and itself. This exclusion is crucial for the fundamental theorem of arithmetic, which we'll discuss shortly.
What is Prime Factorization?
Prime factorization is the process of expressing a composite number (a number that is not prime) as a product of its prime factors. Essentially, it's breaking down a number into its smallest possible prime number components. Every composite number has a unique prime factorization, a property known as the fundamental theorem of arithmetic. This theorem guarantees that regardless of the method used, the prime factorization will always be the same. This uniqueness is a cornerstone of many mathematical proofs and algorithms.
Methods for Finding the Prime Factorization of 192
There are several ways to determine the prime factorization of 192. Let's explore a few common methods:
1. Repeated Division by Prime Numbers
This is a straightforward method. We start by dividing the number by the smallest prime number (2) and continue dividing the result by prime numbers until we are left with 1.
- 192 ÷ 2 = 96
- 96 ÷ 2 = 48
- 48 ÷ 2 = 24
- 24 ÷ 2 = 12
- 12 ÷ 2 = 6
- 6 ÷ 2 = 3
- 3 ÷ 3 = 1
Therefore, the prime factorization of 192 is 2 x 2 x 2 x 2 x 2 x 2 x 3, which can be written more concisely as 2⁶ x 3.
2. Factor Tree
The factor tree method provides a visual representation of the prime factorization process. We start by breaking down the number into any two factors, then continue breaking down those factors until only prime numbers remain.
192
/ \
96 2
/ \
48 2
/ \
24 2
/ \
12 2
/ \
6 2
/ \
3 2
/
1
Following the branches down, we again arrive at the prime factorization: 2⁶ x 3.
3. Using a Calculator or Software
Many calculators and mathematical software packages have built-in functions for prime factorization. These tools are particularly useful for larger numbers where manual methods become tedious. Inputting 192 into such a tool would instantly provide the answer: 2⁶ x 3.
The Significance of Prime Factorization
The seemingly simple act of finding the prime factorization of a number has far-reaching implications across various fields:
1. Cryptography
Prime factorization plays a crucial role in modern cryptography. The security of many encryption algorithms, such as RSA, relies on the difficulty of factoring very large numbers into their prime components. The computational power required to factor extremely large numbers (hundreds or even thousands of digits) is currently beyond the capabilities of even the most powerful computers. This difficulty forms the basis for secure online transactions and data protection.
2. Number Theory
Prime factorization is a fundamental concept in number theory, the branch of mathematics dealing with the properties of integers. Many theorems and conjectures in number theory are directly related to prime numbers and their factorization. For example, the Riemann Hypothesis, one of the most important unsolved problems in mathematics, is concerned with the distribution of prime numbers.
3. Computer Science
Prime factorization algorithms are used in various computer science applications, including:
- Hashing: Prime numbers are often used in hashing algorithms to reduce collisions and improve the efficiency of data storage and retrieval.
- Random Number Generation: Prime numbers play a role in generating pseudo-random numbers, which are crucial for simulations and other computational tasks.
- Data Compression: Some data compression techniques utilize prime numbers to optimize the compression process.
4. Abstract Algebra
In abstract algebra, prime factorization is linked to concepts like unique factorization domains (UFDs), where elements can be uniquely factored into irreducible elements (analogous to prime numbers).
Beyond 192: Exploring Other Factorizations
While we've focused on 192, the principles and methods discussed apply to any composite number. Let's briefly consider the factorization of other numbers to solidify our understanding:
- The prime factorization of 36: 2² x 3²
- The prime factorization of 100: 2² x 5²
- The prime factorization of 1000: 2³ x 5³
- The prime factorization of 1024: 2¹⁰ (a power of 2)
Observing these examples highlights the consistent application of the fundamental theorem of arithmetic – each number has a unique prime factorization.
Conclusion
The prime factorization of 192, 2⁶ x 3, is more than just a simple mathematical result. It serves as an entry point into the fascinating world of number theory and highlights the fundamental importance of prime numbers in mathematics and computer science. Understanding the process of prime factorization, and the various methods for achieving it, builds a crucial foundation for tackling more complex mathematical problems and appreciating the underlying structure of numbers. The seemingly simple question about the prime factorization of 192 reveals the elegant and powerful principles that govern the world of numbers and their applications in numerous fields.
Latest Posts
Latest Posts
-
Transformation Of Energy In A Car
Mar 30, 2025
-
Is Milk A Mixture Or A Solution
Mar 30, 2025
-
Least Common Multiple Of 15 And 27
Mar 30, 2025
-
160 Dollars In Words For Check
Mar 30, 2025
-
Which Of The Following Is A Nonmetal
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about What Is The Prime Factorization Of 192 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
