What Is The Percentage Of 5/12
Juapaving
May 11, 2025 · 5 min read
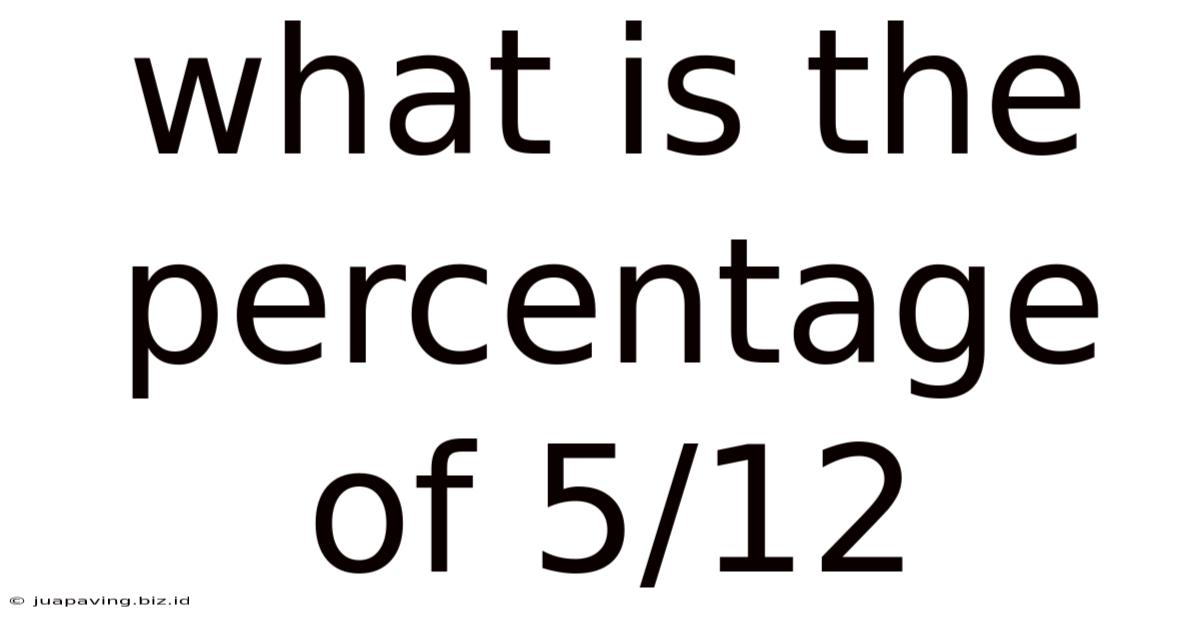
Table of Contents
What is the Percentage of 5/12? A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with applications spanning various fields, from finance and cooking to data analysis and engineering. This comprehensive guide delves into the specifics of converting the fraction 5/12 into a percentage, explaining the process in detail and providing valuable insights into related concepts. We'll explore different methods for calculation, address common misconceptions, and offer practical examples to solidify your understanding. This guide is designed for anyone, from students seeking to improve their math skills to professionals needing a quick refresher on percentage calculations.
Understanding Fractions and Percentages
Before diving into the conversion of 5/12, let's refresh our understanding of fractions and percentages.
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts in the whole. For example, in the fraction 5/12, 5 is the numerator and 12 is the denominator.
Percentages: A percentage represents a fraction of 100. It indicates how many parts out of 100 make up a whole. The symbol "%" denotes a percentage. For instance, 25% means 25 parts out of 100, which can also be written as the fraction 25/100 or the decimal 0.25.
Converting Fractions to Percentages: The Fundamental Process
The core principle behind converting a fraction to a percentage involves expressing the fraction as an equivalent fraction with a denominator of 100. Once you have this equivalent fraction, the numerator represents the percentage. Here's the step-by-step process:
-
Divide the numerator by the denominator: This gives you the decimal equivalent of the fraction.
-
Multiply the decimal by 100: This converts the decimal to a percentage.
Calculating the Percentage of 5/12
Let's apply this process to the fraction 5/12:
-
Divide the numerator by the denominator: 5 ÷ 12 = 0.416666... (The decimal continues infinitely).
-
Multiply the decimal by 100: 0.416666... × 100 = 41.6666...%
Therefore, 5/12 is approximately 41.67%. We typically round to two decimal places for percentage calculations unless greater precision is required.
Alternative Methods for Fraction-to-Percentage Conversion
While the method above is straightforward, other approaches can be equally effective:
-
Using a Calculator: Most calculators have built-in functions for performing fraction-to-percentage conversions directly. Simply enter the fraction (5/12) and use the percentage function.
-
Using Proportions: You can set up a proportion to solve for the percentage. This method is particularly useful for understanding the underlying mathematical relationships. The proportion would look like this:
5/12 = x/100
Solving for x (the percentage), we get:
x = (5 * 100) / 12 = 41.6666...%
Understanding the Remainder and Rounding
Notice that when we divided 5 by 12, we got a repeating decimal (0.416666...). This is a common occurrence when dealing with fractions that don't have a denominator that's a factor of 100 (or 10, 1000, etc.). The remainder signifies the part of the whole that doesn't fit neatly into a percentage divisible by 100. In such cases, we employ rounding to express the percentage to a convenient number of decimal places. Common rounding practices involve rounding to the nearest whole number, tenth, or hundredth.
Practical Applications of Percentage Calculations
The ability to convert fractions to percentages is crucial in numerous practical scenarios:
-
Finance: Calculating interest rates, discounts, profit margins, and tax rates all involve percentage calculations. Understanding how fractions relate to percentages is essential for managing personal finances and making informed business decisions.
-
Data Analysis: When working with data, representing portions as percentages often makes it easier to understand and visualize trends and patterns. Charts and graphs frequently employ percentages to communicate findings effectively.
-
Everyday Life: Percentage calculations are commonly encountered when shopping (sales and discounts), calculating tips, determining grades, and understanding statistics in news reports.
-
Science and Engineering: Many scientific and engineering calculations involve working with fractions and expressing results as percentages. This is particularly relevant in fields like chemistry, physics, and material science where proportions and ratios are frequently utilized.
-
Cooking and Baking: Recipes often specify ingredient quantities as fractions or ratios. Converting these to percentages can improve accuracy and make scaling recipes easier.
Common Misconceptions and Pitfalls
Several common errors can occur when converting fractions to percentages. Here are a few points to keep in mind:
-
Incorrect order of operations: Always perform the division before multiplication when converting a fraction to a percentage.
-
Ignoring the remainder: The remainder should be considered, especially when high accuracy is required. Rounding appropriately maintains accuracy.
-
Confusing fractions and decimals: Ensure you correctly convert the fraction to a decimal before multiplying by 100.
-
Rounding errors: Be aware that rounding can introduce small inaccuracies. The level of accuracy required will determine the appropriate rounding method.
Conclusion: Mastering Percentage Conversions
The ability to convert fractions to percentages is a vital mathematical skill with broad applications across various disciplines. By understanding the fundamental process, exploring different calculation methods, and being aware of potential pitfalls, you can effectively and confidently handle percentage calculations in your personal and professional life. This guide has provided a comprehensive overview of converting the fraction 5/12 to a percentage, emphasizing the importance of understanding the underlying principles and applying them consistently for accurate results. Remember to always check your work and strive for accuracy, recognizing that slight discrepancies can arise due to rounding. With practice, converting fractions to percentages will become second nature.
Latest Posts
Latest Posts
-
How Many Centimeters Are In 8 Dekameters
May 13, 2025
-
Which Of The Following Is A Function Of Lysosomes
May 13, 2025
-
Energy Band Diagram Of A Semiconductor
May 13, 2025
-
Block And Tackle System Of 5 Pulleys
May 13, 2025
-
17 Square Meters In Square Feet
May 13, 2025
Related Post
Thank you for visiting our website which covers about What Is The Percentage Of 5/12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.