What Is The Least Common Multiple Of 9 And 10
Juapaving
Apr 14, 2025 · 4 min read
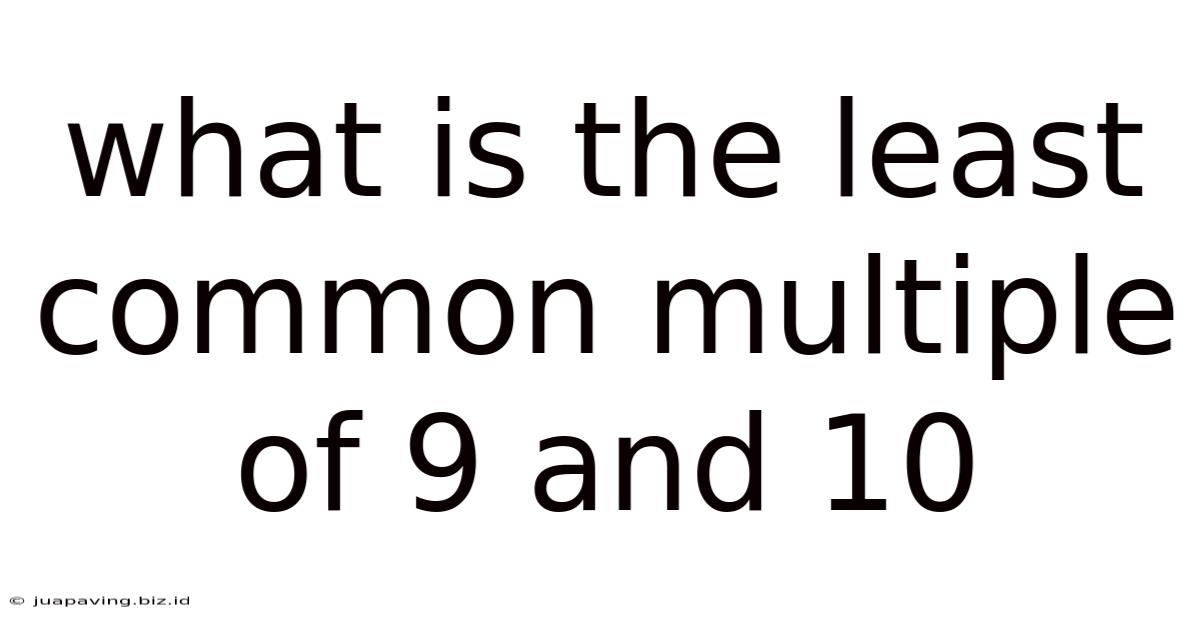
Table of Contents
What is the Least Common Multiple (LCM) of 9 and 10? A Deep Dive into Number Theory
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic problem, but understanding the underlying concepts unlocks a deeper appreciation for number theory and its applications in various fields. This article will explore the LCM of 9 and 10, providing multiple methods for calculation and highlighting the broader significance of this mathematical concept.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the given numbers as factors. This concept is fundamental in various mathematical applications, including:
- Fraction simplification: Finding the LCM of the denominators is crucial when adding or subtracting fractions.
- Scheduling problems: Determining when events will occur simultaneously (e.g., buses arriving at a stop).
- Modular arithmetic: LCM plays a vital role in solving congruences and other problems in modular arithmetic.
- Abstract algebra: The concept extends to more abstract algebraic structures.
Methods for Calculating the LCM of 9 and 10
Several methods can be employed to calculate the LCM of 9 and 10. We'll explore the most common ones:
1. Listing Multiples Method
This is a straightforward approach, especially for smaller numbers:
- List multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, ...
- List multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, ...
By comparing the lists, we observe that the smallest common multiple is 90.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number:
- Prime factorization of 9: 3 x 3 = 3²
- Prime factorization of 10: 2 x 5
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- Highest power of 2: 2¹
- Highest power of 3: 3²
- Highest power of 5: 5¹
Multiply these together: 2 x 3² x 5 = 2 x 9 x 5 = 90
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of two numbers are related by the following formula:
LCM(a, b) x GCD(a, b) = a x b
First, we find the GCD of 9 and 10 using the Euclidean algorithm or prime factorization:
- Prime factorization of 9: 3²
- Prime factorization of 10: 2 x 5
Since there are no common prime factors, the GCD(9, 10) = 1.
Now, using the formula:
LCM(9, 10) = (9 x 10) / GCD(9, 10) = 90 / 1 = 90
This method proves particularly useful when dealing with larger numbers where listing multiples becomes impractical.
The Significance of LCM in Real-World Applications
Beyond the theoretical realm, the LCM finds practical applications in various scenarios:
1. Scheduling and Synchronization
Imagine two buses that leave a terminal at different intervals. One bus leaves every 9 minutes, and the other leaves every 10 minutes. To find out when both buses depart simultaneously, we need to find the LCM of 9 and 10. The LCM (90) indicates that both buses will depart together after 90 minutes.
2. Gear Ratios and Mechanical Systems
In mechanical engineering, gear ratios are often expressed using the LCM to determine the least common speed or rotation. Understanding LCM helps engineers design efficient and synchronized systems.
3. Music and Rhythm
In music theory, the LCM is used to determine the least common denominator for rhythmic patterns and note durations, ensuring harmonious and synchronized musical arrangements.
4. Computer Science and Algorithms
LCM is relevant in various algorithms and data structures. For instance, it plays a crucial role in optimizing array indexing and memory management.
5. Construction and Measurement
In construction, LCM is utilized for precise measurement and material cutting, especially when dealing with different unit sizes.
Exploring Further: Advanced Concepts Related to LCM
The LCM is closely related to other number theory concepts that are worth exploring:
- Greatest Common Divisor (GCD): As demonstrated earlier, the LCM and GCD are intimately linked through a fundamental formula. Understanding GCD enhances the calculation and understanding of LCM.
- Euclidean Algorithm: This efficient algorithm computes the GCD of two integers, and thus indirectly helps in LCM calculations.
- Modular Arithmetic: LCM plays a key role in solving problems involving modular congruences and cyclic patterns.
- Abstract Algebra: The concept of LCM generalizes to other algebraic structures, extending its mathematical significance.
Conclusion: The Power of the LCM
The seemingly simple calculation of the least common multiple of 9 and 10 unveils a rich tapestry of mathematical concepts with far-reaching practical applications. From scheduling problems to gear ratios and musical harmony, the LCM demonstrates its utility in various fields. Mastering the different methods for calculating LCM not only improves mathematical proficiency but also fosters a deeper appreciation for the elegant relationships within number theory. The understanding of the LCM goes beyond simple arithmetic; it's a foundation for more complex mathematical inquiries and problem-solving in diverse real-world scenarios. Further exploration into the related concepts of GCD, modular arithmetic, and abstract algebra only strengthens the significance of this fundamental mathematical concept. By understanding the LCM, we unlock a deeper comprehension of the intricate connections between seemingly simple arithmetic operations and their profound implications across various scientific and engineering disciplines.
Latest Posts
Latest Posts
-
Molar Mass Of Cuso4 X 5h2o
May 09, 2025
-
How To Write 1400 Dollars On A Check
May 09, 2025
-
The Internet Is A Collection Of
May 09, 2025
-
Compute The Volume Of The Prism Shown
May 09, 2025
-
How Many Feet Is 112 In
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 9 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.