What Is The Least Common Multiple Of 14 And 24
Juapaving
Mar 29, 2025 · 5 min read
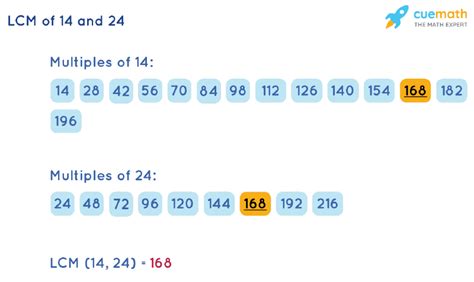
Table of Contents
What is the Least Common Multiple (LCM) of 14 and 24? A Deep Dive into Number Theory
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying principles unlocks a world of applications in mathematics, computer science, and even music theory. This comprehensive guide explores the LCM of 14 and 24, explaining various methods for calculation and delving into the broader significance of LCM in different fields.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
This concept is fundamental in many areas, including:
- Fraction Operations: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
- Scheduling Problems: Determining when events will occur simultaneously (e.g., buses arriving at a stop) often involves LCM calculations.
- Music Theory: LCM is used to determine the least common period of musical rhythms and melodies.
- Computer Science: LCM plays a crucial role in algorithms related to cyclic processes and synchronization.
Calculating the LCM of 14 and 24: Three Methods
There are several ways to calculate the LCM of 14 and 24. Let's explore three common methods:
1. Listing Multiples Method
This is a straightforward approach, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
Multiples of 14: 14, 28, 42, 56, 70, 84, 98, 112, 126, 140, 154, 168...
Multiples of 24: 24, 48, 72, 96, 120, 144, 168...
The smallest multiple common to both lists is 168. Therefore, the LCM(14, 24) = 168.
This method is simple for smaller numbers but becomes impractical for larger numbers.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the highest powers of all prime factors present.
- Prime factorization of 14: 2 x 7
- Prime factorization of 24: 2³ x 3
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3¹ = 3
- Highest power of 7: 7¹ = 7
Multiply these together: 8 x 3 x 7 = 168
Therefore, the LCM(14, 24) = 168. This method is generally more efficient than listing multiples, especially for larger numbers.
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The formula is:
LCM(a, b) = (|a x b|) / GCD(a, b)
First, we need to find the GCD of 14 and 24. We can use the Euclidean algorithm for this:
- Divide 24 by 14: 24 = 14 x 1 + 10
- Divide 14 by 10: 14 = 10 x 1 + 4
- Divide 10 by 4: 10 = 4 x 2 + 2
- Divide 4 by 2: 4 = 2 x 2 + 0
The last non-zero remainder is 2, so GCD(14, 24) = 2.
Now, we can use the formula:
LCM(14, 24) = (14 x 24) / 2 = 336 / 2 = 168
This method provides an alternative approach, particularly useful when dealing with larger numbers where prime factorization might be more cumbersome.
Applications of LCM: Real-World Examples
The LCM isn't just a theoretical concept; it has practical applications in various fields:
1. Scheduling and Synchronization
Imagine two buses arrive at a bus stop. One bus arrives every 14 minutes, and the other arrives every 24 minutes. When will both buses arrive at the bus stop simultaneously? The answer is the LCM(14, 24) = 168 minutes, or 2 hours and 48 minutes.
2. Fraction Addition and Subtraction
Adding fractions with different denominators requires finding a common denominator, which is typically the LCM of the denominators. For example, to add 1/14 and 1/24, we would find the LCM of 14 and 24 (168), convert the fractions to equivalent fractions with a denominator of 168, and then add them.
3. Gear Ratios and Rotational Mechanics
In mechanical engineering, gear ratios and rotational speeds often rely on LCM calculations to determine synchronization and optimal performance.
4. Music Theory and Rhythm
In music, the LCM helps determine when different rhythmic patterns will align. For instance, if one musical phrase repeats every 14 beats and another repeats every 24 beats, they will coincide every 168 beats.
5. Computer Science and Cyclic Processes
In programming and computer science, LCM is used in algorithms dealing with cyclic processes and synchronization issues, ensuring that different processes align correctly.
Advanced Concepts Related to LCM
Understanding LCM opens doors to more advanced mathematical concepts:
- Least Common Multiple of More Than Two Numbers: The principles extend to finding the LCM of multiple numbers. The prime factorization method remains efficient for this.
- Relationship between LCM and GCD: The relationship LCM(a, b) x GCD(a, b) = a x b is a fundamental identity in number theory.
- Applications in Abstract Algebra: LCM and GCD concepts extend into abstract algebra and ring theory, providing valuable tools for analysis.
Conclusion: The Importance of Understanding LCM
The seemingly simple concept of the least common multiple has far-reaching implications across various disciplines. By mastering the different methods of calculating the LCM, and understanding its applications, you equip yourself with a powerful tool for solving problems in mathematics, computer science, engineering, and even music. The journey from finding the LCM of 14 and 24 to grasping its broader significance highlights the beauty and practical utility of fundamental mathematical principles. The ability to efficiently calculate and apply the LCM demonstrates a robust understanding of number theory and its real-world applications, skills highly valued across many professional fields.
Latest Posts
Latest Posts
-
The Clavicle Articulates With The Sternum And The Scapula
Mar 31, 2025
-
Is Oxygen A Metal Nonmetal Or Metalloid
Mar 31, 2025
-
Keyboard Is A Hardware Or Software
Mar 31, 2025
-
Is 45 A Multiple Of 9
Mar 31, 2025
-
Forward Primer And Reverse Primer In Pcr
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 14 And 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
