What Is The Lcm Of 8 And 2
Juapaving
Apr 04, 2025 · 5 min read
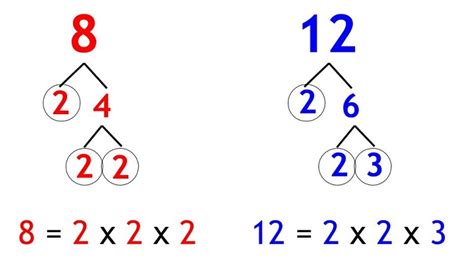
Table of Contents
What is the LCM of 8 and 2? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly in arithmetic and number theory. It has wide-ranging applications in various fields, from simplifying fractions to solving complex problems in engineering and computer science. This article will thoroughly explore the concept of LCM, focusing specifically on finding the LCM of 8 and 2, and extending the understanding to more complex scenarios. We'll delve into different methods for calculating the LCM, providing a comprehensive guide suitable for students, teachers, and anyone seeking a better grasp of this mathematical concept.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. For example, the LCM of 3 and 5 is 15 because 15 is the smallest positive integer that is divisible by both 3 and 5.
Understanding LCM is crucial for several reasons:
- Simplifying Fractions: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
- Solving Problems Involving Ratios and Proportions: Many real-world problems involving ratios and proportions require finding the LCM to determine the smallest common quantity.
- Scheduling and Cyclical Events: LCM is essential in solving problems related to scheduling events that repeat at different intervals, such as the timing of traffic lights or the synchronization of machinery.
- Modular Arithmetic: LCM plays a vital role in modular arithmetic, a branch of number theory used in cryptography and other areas of computer science.
Calculating the LCM of 8 and 2
Now let's tackle the specific problem: finding the LCM of 8 and 2. There are several ways to do this:
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 8: 8, 16, 24, 32, 40, 48...
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18...
By comparing the lists, we see that the smallest multiple common to both 8 and 2 is 8. Therefore, the LCM of 8 and 2 is 8.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves expressing each number as a product of its prime factors.
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 2: 2
To find the LCM using prime factorization, we identify the highest power of each prime factor present in either number. In this case, the only prime factor is 2, and the highest power is 2³.
Therefore, LCM(8, 2) = 2³ = 8.
Method 3: Using the Formula (for two numbers)
For two numbers 'a' and 'b', there's a formula relating the LCM and the greatest common divisor (GCD):
LCM(a, b) = (|a x b|) / GCD(a, b)
First, we need to find the GCD (greatest common divisor) of 8 and 2. The GCD is the largest number that divides both 8 and 2 without leaving a remainder. In this case, the GCD(8, 2) = 2.
Now, we can apply the formula:
LCM(8, 2) = (|8 x 2|) / GCD(8, 2) = 16 / 2 = 8
Extending the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. Let's consider finding the LCM of 8, 2, and 12.
Method 1: Listing Multiples (Less Efficient for More Numbers)
Listing multiples becomes cumbersome with more numbers. While possible, it's not the most efficient approach for three or more numbers.
Method 2: Prime Factorization (Most Efficient)
This method remains the most efficient for multiple numbers.
- Prime factorization of 8: 2³
- Prime factorization of 2: 2
- Prime factorization of 12: 2² x 3
We identify the highest power of each prime factor present:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3¹ = 3
Therefore, LCM(8, 2, 12) = 2³ x 3 = 8 x 3 = 24
Method 3: Stepwise Approach Using the Formula (for more than two numbers)
You can calculate the LCM iteratively. First, find the LCM of two numbers, then find the LCM of that result and the next number, and so on.
- LCM(8, 2) = 8 (as calculated previously)
- LCM(8, 12) = (|8 x 12|) / GCD(8, 12) = 96 / 4 = 24
Real-World Applications of LCM
The LCM has practical applications in diverse fields:
-
Construction and Engineering: Determining the optimal length of materials, coordinating the timing of machinery, and planning construction schedules often involve finding the LCM. For instance, if two conveyor belts have different cycle times, finding the LCM helps determine when both belts will complete a cycle simultaneously.
-
Scheduling and Time Management: Planning recurring events, like meetings or deliveries, with different frequencies requires the LCM. If one event happens every 8 days and another every 2 days, they will coincide every 8 days (the LCM of 8 and 2).
-
Music and Rhythm: In music theory, the LCM is used to determine the least common multiple of the rhythmic values of different notes, aiding in composition and harmony.
-
Computer Science: LCM finds applications in algorithm design, particularly in problems involving synchronization and scheduling of processes.
-
Cooking and Baking: Scaling up recipes often involves finding the LCM to ensure consistent ratios of ingredients.
Conclusion
Understanding and calculating the least common multiple is a fundamental skill in mathematics with broad applications. While listing multiples is a simple method for smaller numbers, prime factorization provides a more efficient and robust approach, especially when dealing with larger numbers or multiple numbers. Mastering the LCM concept enhances problem-solving abilities in various contexts, from everyday situations to complex scientific and engineering challenges. Remember that the LCM of 8 and 2, as demonstrated through various methods, is definitively 8. This seemingly simple calculation forms the foundation for understanding more intricate mathematical concepts and real-world applications.
Latest Posts
Latest Posts
-
As The Concentration Of An Electrolyte Reduces The Conductivity
Apr 05, 2025
-
Class 10 History Ch 2 Notes
Apr 05, 2025
-
An Example Of An Oil In Water Emulsion Is
Apr 05, 2025
-
Ficks Law Of Diffusion Transcellular Pathway
Apr 05, 2025
-
What Is The Least Common Multiple Of 12 And 4
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 8 And 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
