What Is The Lcm Of 4 And 5
Juapaving
Apr 01, 2025 · 5 min read
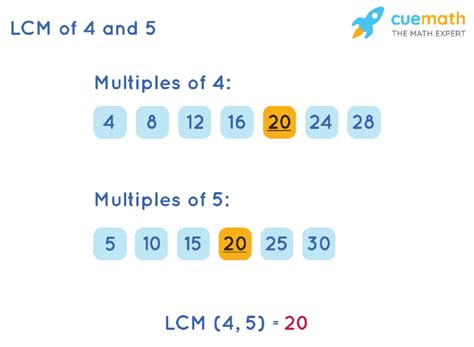
Table of Contents
What is the LCM of 4 and 5? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex algebraic equations. This article will explore the LCM of 4 and 5, providing a comprehensive understanding of the process and illustrating its broader significance within the field of mathematics. We'll delve into different methods for calculating the LCM, discuss its relationship to the greatest common divisor (GCD), and showcase real-world examples where this seemingly simple calculation holds significant weight.
Understanding Least Common Multiples (LCM)
Before diving into the specific LCM of 4 and 5, let's establish a firm understanding of the concept itself. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers as factors.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12, and so on. Multiples of 3 are 3, 6, 9, 12, 15, and so on. The common multiples of 2 and 3 are 6, 12, 18, and so on. The least common multiple, therefore, is 6.
Calculating the LCM of 4 and 5: Method 1 - Listing Multiples
The most straightforward method for finding the LCM of relatively small numbers like 4 and 5 is by listing their multiples. Let's do this:
Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40...
Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40...
By comparing the two lists, we can see that the smallest number present in both lists is 20. Therefore, the LCM of 4 and 5 is 20.
This method is simple and intuitive, especially for smaller numbers. However, it becomes less practical when dealing with larger numbers or a greater quantity of numbers.
Calculating the LCM of 4 and 5: Method 2 - Prime Factorization
A more efficient and versatile method for finding the LCM, especially for larger numbers, involves prime factorization. This method breaks down each number into its prime factors – numbers divisible only by 1 and themselves.
- Prime factorization of 4: 2 x 2 = 2²
- Prime factorization of 5: 5 (5 is a prime number)
To find the LCM using prime factorization, we identify the highest power of each prime factor present in either factorization:
- The highest power of 2 is 2² = 4
- The highest power of 5 is 5¹ = 5
Now, we multiply these highest powers together: 4 x 5 = 20. Therefore, the LCM of 4 and 5 is again 20.
This method is significantly more efficient for larger numbers because it avoids the tedious process of listing multiples. It provides a systematic and structured approach that scales well to more complex problems.
Calculating the LCM of 4 and 5: Method 3 - Using the GCD
The greatest common divisor (GCD) and the least common multiple (LCM) are closely related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
where 'a' and 'b' are the two numbers.
First, let's find the GCD of 4 and 5. The GCD is the largest number that divides both 4 and 5 without leaving a remainder. In this case, the only number that divides both 4 and 5 is 1. Therefore, GCD(4, 5) = 1.
Now, we can use the formula:
LCM(4, 5) x GCD(4, 5) = 4 x 5 LCM(4, 5) x 1 = 20 LCM(4, 5) = 20
This method highlights the interconnectedness between GCD and LCM. Knowing one allows you to easily calculate the other. This approach is particularly useful when dealing with larger numbers where finding the GCD using the Euclidean algorithm might be more efficient than directly calculating the LCM through prime factorization or listing multiples.
Real-World Applications of LCM
While the LCM of 4 and 5 might seem like a simple mathematical exercise, understanding and applying the concept of LCM has numerous real-world implications:
-
Scheduling: Imagine you have two machines that operate on different cycles. One completes a cycle every 4 hours, and the other every 5 hours. To determine when both machines will complete a cycle simultaneously, you need to find the LCM(4, 5) = 20. Both machines will complete a cycle at the same time after 20 hours.
-
Fraction Simplification: When adding or subtracting fractions, finding the LCM of the denominators is crucial to obtain a common denominator. This simplifies the calculation significantly.
-
Music Theory: LCM is essential in music theory for determining the least common multiple of note durations or rhythmic patterns, useful in harmonizing different musical lines.
-
Construction and Engineering: LCM is applicable in situations requiring synchronized actions or periodic events, like the timing of machinery in assembly lines or the timing of signals in traffic light systems.
-
Project Management: In scheduling multiple project phases with varying durations, finding the LCM of the project durations can be used to optimize the overall timeline and resource allocation.
Expanding the Concept: LCM of More Than Two Numbers
The methods discussed above can be extended to calculate the LCM of more than two numbers. For the prime factorization method, you would consider the highest power of each prime factor present in the factorization of all the numbers. For the method involving GCD, you would need to apply the GCD and LCM relationships iteratively.
For instance, to find the LCM of 4, 5, and 6, we would perform the following:
- Prime factorization:
- 4 = 2²
- 5 = 5
- 6 = 2 x 3
- Highest powers of prime factors: 2², 3, 5
- LCM(4, 5, 6) = 2² x 3 x 5 = 60
Conclusion
Determining the least common multiple (LCM) is a fundamental skill in mathematics with broad practical applications. While the LCM of 4 and 5, which is 20, might seem a simple calculation, understanding the underlying principles and different methods – listing multiples, prime factorization, and using the GCD – equips you to tackle more complex LCM problems efficiently. This understanding becomes essential when dealing with various mathematical and real-world scenarios requiring synchronized events, fraction simplification, and optimized scheduling. The methods and examples provided in this article demonstrate the versatility and importance of LCM across multiple disciplines. The ability to calculate LCM, along with the related concept of GCD, is a valuable asset in any mathematical toolkit.
Latest Posts
Latest Posts
-
How Many Mm Is 3 Cm
Apr 02, 2025
-
A Red Blood Cell Placed In A Hypertonic Medium Will
Apr 02, 2025
-
What Is The Conjugate Acid Of Nh3
Apr 02, 2025
-
What Is Central Bureau Of Investigation
Apr 02, 2025
-
How Many Ml Is 1 75 Liters
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 4 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
