What Is The Lcm For 3 And 4
Juapaving
Mar 29, 2025 · 5 min read
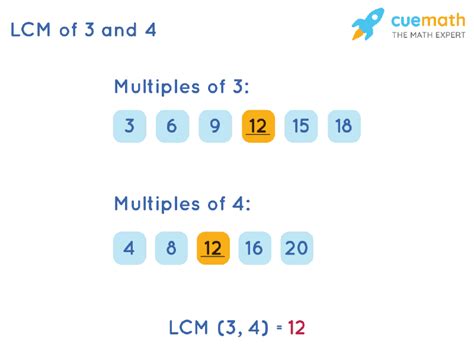
Table of Contents
What is the LCM for 3 and 4? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly useful in various fields like fractions, scheduling, and even music theory. This article will thoroughly explore how to calculate the LCM for 3 and 4, and then delve deeper into the broader concept of LCM, providing you with a solid understanding of the topic.
Understanding Least Common Multiples (LCM)
Before we dive into the specific example of 3 and 4, let's define what a least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
For instance, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16... and multiples of 3 are 3, 6, 9, 12, 15, 18... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Calculating the LCM of 3 and 4
Now, let's tackle the question at hand: what is the LCM of 3 and 4?
We can use a few different methods to find the LCM of 3 and 4:
Method 1: Listing Multiples
The simplest method, especially for smaller numbers, is to list the multiples of each number until we find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, ...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, ...
As you can see, the smallest number that appears in both lists is 12. Therefore, the LCM of 3 and 4 is 12.
Method 2: Prime Factorization
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor.
- Prime factorization of 3: 3 (3 is a prime number)
- Prime factorization of 4: 2 x 2 = 2²
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3¹ = 3
Multiply these together: 4 x 3 = 12. Therefore, the LCM of 3 and 4 is 12.
Method 3: Using the Formula (for two numbers)
For two numbers a and b, the LCM can be calculated using the formula:
LCM(a, b) = (|a * b|) / GCD(a, b)
where GCD(a, b) is the greatest common divisor of a and b.
Let's apply this to 3 and 4:
-
Find the GCD of 3 and 4: The greatest common divisor of 3 and 4 is 1 (because 1 is the only common divisor).
-
Apply the formula: LCM(3, 4) = (3 * 4) / 1 = 12
Therefore, the LCM of 3 and 4 is 12.
Applications of LCM
The concept of LCM has far-reaching applications across various fields:
1. Fraction Addition and Subtraction
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial. The LCM becomes the least common denominator (LCD), allowing you to rewrite the fractions with a common denominator before performing the addition or subtraction.
Example: Adding 1/3 + 1/4. The LCM of 3 and 4 is 12. We rewrite the fractions as 4/12 + 3/12 = 7/12.
2. Scheduling Problems
LCM is frequently used to solve scheduling problems. For example, if two events occur at regular intervals (e.g., buses leaving a station every 3 minutes and 4 minutes respectively), the LCM determines when both events will occur simultaneously. In this case, the buses will coincide every 12 minutes.
3. Music Theory
In music, the LCM helps determine the least common multiple of note durations. This is particularly useful in understanding rhythmic patterns and harmonization. For instance, understanding the LCM of different note values (whole, half, quarter, etc.) is crucial for composing and understanding musical structure.
4. Gear Ratios and Mechanical Engineering
In mechanical systems involving gears, the LCM helps calculate the timing and synchronization of rotating components. The ratio of gear teeth and their LCM determine how often the gears will align perfectly. This is vital in designing efficient and reliable machinery.
5. Cyclic Events and Pattern Recognition
LCM plays a significant role in identifying patterns and cycles in data analysis. This could be applied to predicting periodic events, analyzing cyclical time series data (like seasonal sales figures), or identifying patterns in natural phenomena.
Finding LCM for More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. The prime factorization method is particularly useful in these cases.
Example: Finding the LCM of 3, 4, and 6
-
Prime Factorization:
- 3 = 3
- 4 = 2²
- 6 = 2 x 3
-
Identify highest powers: The highest power of 2 is 2², and the highest power of 3 is 3.
-
Calculate LCM: 2² x 3 = 4 x 3 = 12. Therefore, the LCM of 3, 4, and 6 is 12.
Conclusion
Understanding the concept of Least Common Multiple is a fundamental skill in mathematics with far-reaching applications. Whether you're dealing with fractions, scheduling problems, or more complex scenarios, mastering the techniques to calculate the LCM will prove invaluable. This article has explored the calculation of the LCM for 3 and 4 through various methods and highlighted the broader significance of LCM in different fields. Remember that choosing the appropriate method depends on the numbers involved and the complexity of the problem. For smaller numbers, listing multiples is often the easiest approach, while prime factorization becomes increasingly efficient for larger numbers or when dealing with multiple numbers simultaneously.
Latest Posts
Latest Posts
-
Solve The Equation Round To The Nearest Hundredth
Mar 31, 2025
-
A Tool With A Curved Blade
Mar 31, 2025
-
In Situ And Ex Situ Conservation
Mar 31, 2025
-
As You Move Left To Right On The Periodic Table
Mar 31, 2025
-
What Is The Chemical Formula For Photosynthesis And Cellular Respiration
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm For 3 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
