What Is The Interior Angle Sum Of A Regular Hexagon
Juapaving
Mar 30, 2025 · 5 min read
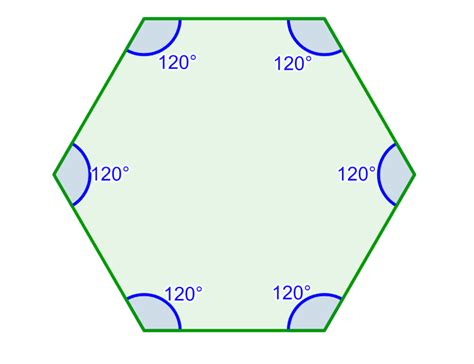
Table of Contents
What is the Interior Angle Sum of a Regular Hexagon? A Comprehensive Guide
Understanding the interior angle sum of polygons, especially regular ones like the hexagon, is fundamental to geometry. This comprehensive guide will delve deep into the concept, exploring various methods to calculate the interior angle sum of a regular hexagon, and expanding on related geometrical principles. We'll also look at how to calculate individual interior angles and exterior angles, and explore applications of this knowledge.
Understanding Polygons and Their Angles
Before jumping into hexagons, let's establish a firm understanding of polygons in general. A polygon is a closed two-dimensional figure formed by connecting straight line segments. These segments are called sides, and the points where the sides meet are called vertices. Polygons are classified based on the number of sides they possess:
- Triangle: 3 sides
- Quadrilateral: 4 sides
- Pentagon: 5 sides
- Hexagon: 6 sides
- Heptagon: 7 sides
- Octagon: 8 sides
- And so on...
Regular polygons are polygons where all sides are of equal length, and all interior angles are equal in measure. Irregular polygons, on the other hand, have sides and angles of varying lengths and measures.
Interior Angles vs. Exterior Angles
Every polygon has both interior and exterior angles. An interior angle is an angle formed inside the polygon by two adjacent sides. An exterior angle is formed by extending one side of the polygon and measuring the angle between the extended side and the adjacent side. The sum of an interior angle and its corresponding exterior angle is always 180 degrees.
Calculating the Interior Angle Sum of a Hexagon: The Formula Approach
The most efficient way to determine the interior angle sum of any polygon is using a formula. This formula relies on the number of sides (n) the polygon possesses:
Interior Angle Sum = (n - 2) * 180°
For a hexagon, which has 6 sides (n = 6), the calculation is straightforward:
Interior Angle Sum = (6 - 2) * 180° = 4 * 180° = 720°
Therefore, the sum of the interior angles of any hexagon, whether regular or irregular, is always 720 degrees. This is a fundamental property of hexagons.
Calculating the Interior Angle Sum of a Hexagon: The Triangulation Method
Another method to calculate the interior angle sum involves dividing the hexagon into triangles. This method provides a visual and intuitive understanding of the formula.
Imagine drawing lines from one vertex of the hexagon to all other non-adjacent vertices. This divides the hexagon into four triangles. Since the sum of the interior angles of a triangle is always 180°, the total sum of the interior angles of the four triangles is 4 * 180° = 720°. This is the same result we obtained using the formula. This triangulation method works for any polygon; the number of triangles always equals (n-2), where n is the number of sides.
Calculating Individual Interior Angles of a Regular Hexagon
While the total sum of interior angles is 720° for any hexagon, the measure of each individual interior angle differs depending on whether the hexagon is regular or irregular. For a regular hexagon, all interior angles are equal. To find the measure of each individual angle, simply divide the total sum by the number of angles (which is equal to the number of sides):
Individual Interior Angle = Total Interior Angle Sum / Number of Sides = 720° / 6 = 120°
Each interior angle of a regular hexagon measures 120 degrees.
Calculating Exterior Angles of a Regular Hexagon
As mentioned earlier, the sum of an interior angle and its corresponding exterior angle is always 180°. Since each interior angle of a regular hexagon is 120°, each exterior angle is:
Exterior Angle = 180° - Interior Angle = 180° - 120° = 60°
The sum of the exterior angles of any polygon, regardless of whether it's regular or irregular, always equals 360°. For a regular hexagon, this is 6 * 60° = 360°.
Applications of Hexagon Geometry
Understanding the properties of hexagons, particularly their interior angle sums, has numerous applications in various fields:
1. Architecture and Design
Hexagons are frequently used in architectural and design applications due to their efficient space-filling properties. Honeycombs, for example, are natural examples of hexagonal structures. The equal angles and sides of a regular hexagon make it ideal for creating stable and aesthetically pleasing structures.
2. Engineering
Hexagonal shapes are used in engineering for creating strong and durable structures. The equal angles and sides of a regular hexagon distribute stress evenly, making it a useful shape for building components and parts.
3. Computer Graphics and Game Design
Hexagonal grids are commonly used in computer graphics and game design to create maps and game boards. The six-sided nature of hexagons allows for smooth transitions and efficient pathfinding algorithms.
4. Nature
Hexagons appear naturally in various contexts, like the hexagonal columns in basalt formations and the hexagonal cells in honeycombs. These natural occurrences demonstrate the efficiency and stability of the hexagonal shape.
Further Exploration: Irregular Hexagons
While our focus has been on regular hexagons, it's important to remember that the interior angle sum (720°) applies to all hexagons, even irregular ones. The difference lies in the individual angle measures. In irregular hexagons, the angles will have different values, but their sum will always remain 720°. Calculating the individual angles of an irregular hexagon requires more information, such as the lengths of its sides or the measures of some of its angles.
Conclusion: Mastering Hexagon Geometry
Understanding the interior angle sum of a regular hexagon is a fundamental concept in geometry. Whether you use the formula or the triangulation method, the result remains consistent: 720°. This knowledge extends beyond theoretical understanding, offering practical applications in diverse fields, from architecture and engineering to computer graphics and even the natural world. By grasping the principles discussed here, you've taken a significant step towards a deeper appreciation of geometric shapes and their properties. Remember to practice applying these concepts to various problems to further solidify your understanding. From the simple act of calculating angles to the complex applications in advanced fields, the hexagon's geometry continues to inspire and inform.
Latest Posts
Latest Posts
-
Why Is Burning A Chemical Change
Apr 01, 2025
-
How Many Years Are In One Millennia
Apr 01, 2025
-
Whats The Difference Between Electron Geometry And Molecular Geometry
Apr 01, 2025
-
Which Is Not A Nucleotide Found In Dna
Apr 01, 2025
-
5 Letter Words Starting With A S
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Interior Angle Sum Of A Regular Hexagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
