What Is Lcm Of 9 And 12
Juapaving
Mar 26, 2025 · 5 min read
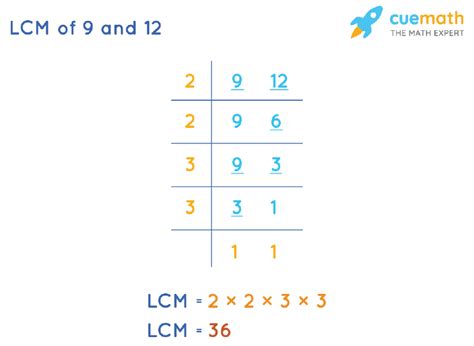
Table of Contents
What is the LCM of 9 and 12? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly useful in arithmetic, algebra, and even more advanced fields. Understanding how to calculate the LCM is crucial for solving various problems, from simplifying fractions to coordinating schedules. This article will provide a comprehensive explanation of how to find the LCM of 9 and 12, exploring multiple methods and demonstrating their practical applications. We'll also delve into the underlying mathematical principles and address common misconceptions.
Understanding Least Common Multiples (LCM)
Before we tackle the specific example of 9 and 12, let's define what the LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that both (or all) numbers divide into evenly without leaving a remainder.
Key Concepts:
- Multiple: A multiple of a number is the product of that number and any integer. For example, multiples of 9 are 9, 18, 27, 36, 45, and so on.
- Common Multiple: A common multiple of two or more numbers is a number that is a multiple of all of them. For instance, common multiples of 9 and 12 include 36, 72, 108, etc.
- Least Common Multiple (LCM): The smallest of these common multiples is the LCM.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers like 9 and 12. We simply list the multiples of each number until we find the smallest common multiple.
Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81...
Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96...
By comparing the lists, we see that the smallest number appearing in both lists is 36. Therefore, the LCM of 9 and 12 is 36.
Advantages: Simple and easy to understand, particularly for beginners.
Disadvantages: Inefficient for larger numbers or when dealing with more than two numbers. It can become tedious and time-consuming.
Method 2: Prime Factorization
This method is more efficient and systematic, especially when dealing with larger numbers or multiple numbers. It involves breaking down each number into its prime factors.
Prime Factorization of 9:
9 = 3 x 3 = 3²
Prime Factorization of 12:
12 = 2 x 2 x 3 = 2² x 3
Finding the LCM using Prime Factorization:
- Identify the prime factors of each number.
- For each prime factor, take the highest power that appears in any of the factorizations.
- Multiply these highest powers together to find the LCM.
In our case:
- The prime factors are 2 and 3.
- The highest power of 2 is 2² = 4.
- The highest power of 3 is 3² = 9.
Therefore, the LCM(9, 12) = 2² x 3² = 4 x 9 = 36.
Advantages: More efficient and systematic than listing multiples, especially for larger numbers. Works well with multiple numbers.
Disadvantages: Requires knowledge of prime factorization.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD) are closely related. There's a useful formula that connects them:
LCM(a, b) = (|a x b|) / GCD(a, b)
Where:
- a and b are the two numbers.
- |a x b| represents the absolute value of the product of a and b.
- GCD(a, b) is the greatest common divisor of a and b.
First, let's find the GCD of 9 and 12 using the Euclidean algorithm:
- Divide the larger number (12) by the smaller number (9): 12 ÷ 9 = 1 with a remainder of 3.
- Replace the larger number with the smaller number (9) and the smaller number with the remainder (3): 9 ÷ 3 = 3 with a remainder of 0.
- The last non-zero remainder is the GCD, which is 3.
Now, we can use the formula:
LCM(9, 12) = (9 x 12) / GCD(9, 12) = 108 / 3 = 36
Advantages: Efficient for larger numbers, leverages the readily available GCD calculation methods.
Disadvantages: Requires understanding of both LCM and GCD concepts and their relationship.
Applications of LCM
Understanding LCM has numerous applications across various mathematical and real-world scenarios:
-
Fraction Addition and Subtraction: Finding the LCM of the denominators is crucial for adding or subtracting fractions with unlike denominators. For example, to add 1/9 and 1/12, you'd find the LCM (36) and rewrite the fractions with this common denominator before adding.
-
Scheduling and Time Problems: The LCM is useful in solving problems involving cyclical events that need to be synchronized. For example, two buses leave a station at different intervals; finding the LCM of these intervals helps determine when they'll depart at the same time again.
-
Modular Arithmetic: LCM plays a significant role in modular arithmetic, a branch of number theory with applications in cryptography and computer science.
-
Algebra and Number Theory: LCM concepts are foundational to more advanced mathematical topics.
Common Mistakes to Avoid
-
Confusing LCM and GCD: Many students confuse LCM and GCD. Remember, the LCM is the smallest common multiple, while the GCD is the greatest common divisor.
-
Incorrect Prime Factorization: Ensure you correctly identify the prime factors of each number to accurately calculate the LCM using prime factorization.
-
Errors in Calculation: Double-check your calculations, especially when using the GCD method, to avoid errors in dividing or multiplying.
Conclusion: Mastering the LCM
Finding the LCM of 9 and 12, as demonstrated through various methods, reinforces the importance of understanding this fundamental mathematical concept. While the listing method is straightforward for smaller numbers, prime factorization and the GCD method provide more efficient and systematic approaches for larger and more complex scenarios. Mastering LCM calculation opens doors to tackling more advanced mathematical problems and solving practical real-world challenges related to scheduling, fractions, and various other applications. By understanding the underlying principles and avoiding common pitfalls, you can confidently apply LCM calculations in diverse contexts. Remember to choose the method that best suits the numbers involved and your level of mathematical comfort. The key is to develop a solid understanding of the concept and its practical applications.
Latest Posts
Latest Posts
-
What Can 18 Be Divided By
Mar 29, 2025
-
A Piece Of Land Almost Surrounded By Water
Mar 29, 2025
-
How Many Cm Is 2 Meters
Mar 29, 2025
-
A Fraction With Numerator 1 Is Called
Mar 29, 2025
-
What Is The Value Of N
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Is Lcm Of 9 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
