A Fraction With Numerator 1 Is Called
Juapaving
Mar 29, 2025 · 6 min read
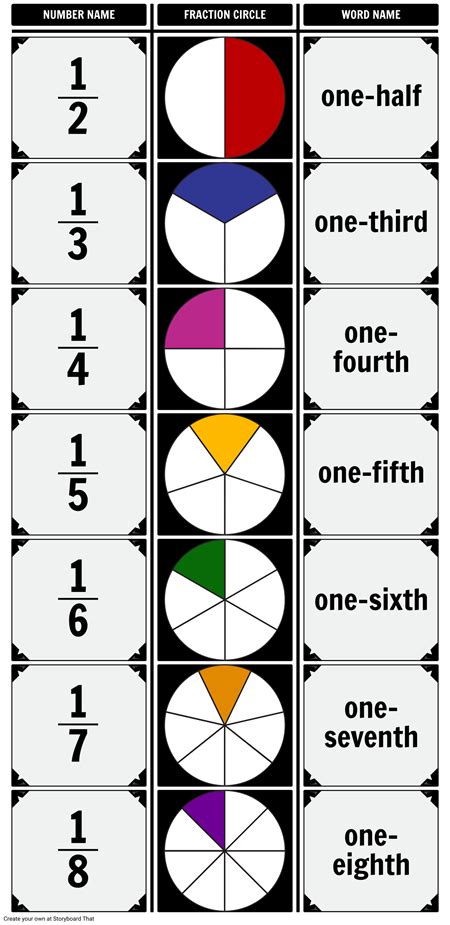
Table of Contents
A Fraction with Numerator 1 is Called a Unit Fraction: A Deep Dive
A fraction with a numerator of 1 is known as a unit fraction. This seemingly simple concept underpins a surprising wealth of mathematical ideas, from ancient Egyptian arithmetic to modern number theory. This article will explore unit fractions in detail, examining their properties, historical significance, and applications in various mathematical fields. We'll delve into their representation, operations, and the unique challenges and insights they offer.
Understanding Unit Fractions: The Basics
A unit fraction is a rational number expressed in the form 1/n, where 'n' is any positive integer greater than 1. This means the numerator is always 1, while the denominator can be any whole number. Examples of unit fractions include:
- 1/2 (one-half)
- 1/3 (one-third)
- 1/4 (one-quarter)
- 1/5 (one-fifth)
- 1/100 (one-hundredth)
- 1/1000 (one-thousandth)
and so on. The key characteristic is that these fractions represent a single part of a whole that has been divided into 'n' equal parts.
Historical Significance: The Egyptians and Unit Fractions
Unit fractions hold a special place in the history of mathematics. Ancient Egyptians developed a unique system of fractions that relied almost exclusively on unit fractions and the fraction 2/3. Their mathematical texts, such as the Rhind Papyrus, reveal sophisticated techniques for representing other fractions as sums of distinct unit fractions. For instance, they wouldn't write 2/5 as a single fraction; instead, they would express it as the sum of two unit fractions: 1/3 + 1/15.
This approach, while seemingly cumbersome by modern standards, showcased a deep understanding of fractional arithmetic. The Egyptians lacked the notation and conceptual framework that allowed for the use of more complex fractions as we know them today. Their reliance on unit fractions spurred the development of algorithms and techniques for decomposing fractions into unit fraction sums. This unique system highlights the versatility and significance of unit fractions even in the absence of a more advanced fractional notation.
The Rhind Papyrus and Unit Fraction Decomposition
The Rhind Papyrus, a significant ancient Egyptian mathematical text, contains a table of decompositions of fractions of the form 2/n into sums of distinct unit fractions. This table demonstrates the Egyptians' mastery of working with unit fractions and their ability to solve complex problems using only unit fractions. Analyzing this papyrus gives invaluable insights into their mathematical thought process and their practical applications of unit fractions in daily life, such as in land measurement and distribution of goods. The algorithms used in these decompositions are still studied today, showcasing the elegance and efficiency of the Egyptian methods.
Properties and Characteristics of Unit Fractions
Unit fractions possess several unique properties that make them an interesting area of study:
-
Reciprocal Relationship: A unit fraction is simply the reciprocal of a positive integer. The reciprocal of a number is obtained by dividing 1 by that number. Therefore, the reciprocal of 'n' is 1/n, which is a unit fraction.
-
Monotonically Decreasing: As the denominator 'n' increases, the value of the unit fraction 1/n decreases. This property is intuitively clear: 1/2 is greater than 1/3, which is greater than 1/4, and so on.
-
Density: Unit fractions are dense in the interval (0,1]. This means that for any two unit fractions, no matter how close they are to each other, there always exists another unit fraction between them.
-
Approximation: Unit fractions can be used to approximate other fractions and real numbers. This is particularly useful in scenarios where simple approximations are preferred over more complex expressions.
Operations with Unit Fractions
While addition and subtraction of unit fractions can sometimes lead to relatively straightforward calculations, multiplication and division can result in more complex expressions.
Addition and Subtraction
Adding or subtracting unit fractions with different denominators often requires finding a common denominator. For example:
1/2 + 1/3 = (3 + 2)/6 = 5/6
1/4 - 1/8 = (2 - 1)/8 = 1/8
However, the sum of two distinct unit fractions is generally not a unit fraction.
Multiplication and Division
Multiplying unit fractions is relatively straightforward:
(1/a) * (1/b) = 1/(ab)
The result is still a unit fraction, although the denominator is the product of the original denominators.
Division of unit fractions involves reciprocating the divisor and multiplying:
(1/a) / (1/b) = (1/a) * (b/1) = b/a
The result may or may not be a unit fraction, depending on whether 'b' is a multiple of 'a'.
Applications of Unit Fractions
Despite their apparent simplicity, unit fractions have found applications in various areas:
-
Music Theory: Unit fractions are used to define musical intervals and ratios in various musical scales and tuning systems.
-
Computer Science: Unit fractions can appear in algorithms and data structures, particularly in situations involving discrete mathematics and graph theory.
-
Approximation Theory: The use of unit fractions for approximating other fractions or real numbers forms the basis of certain approximation algorithms.
-
Number Theory: Research into unit fractions is closely tied to number theory problems relating to the representation of rational numbers as sums of unit fractions, a field with ongoing research and unresolved conjectures.
-
Egyptian Fraction Representation: The ancient Egyptian method of representing fractions as sums of distinct unit fractions continues to be a topic of mathematical interest and study, with algorithms being developed to efficiently generate such representations.
Unique Challenges and Advanced Topics
While seemingly basic, unit fractions present some interesting mathematical challenges:
-
Erdős–Straus Conjecture: This unsolved conjecture in number theory states that every fraction of the form 4/n (where n is an integer greater than 1) can be expressed as the sum of at most three unit fractions. It remains an open problem, highlighting the surprising depth hidden within the seemingly simple world of unit fractions.
-
Optimal Unit Fraction Representations: Finding the most efficient way to represent a fraction as a sum of unit fractions, meaning the representation with the fewest number of terms, is a computationally complex problem with ongoing research.
-
Continued Fractions and Unit Fractions: The relationship between continued fractions and unit fractions is an area of study exploring the connection between these different representations of rational numbers.
Conclusion: The Enduring Relevance of Unit Fractions
The seemingly simple unit fraction, represented as 1/n, holds a profound significance in the history and ongoing development of mathematics. From its crucial role in ancient Egyptian arithmetic to its continued relevance in modern number theory and other mathematical fields, the unit fraction provides a rich area of exploration and discovery. Its properties, applications, and associated unsolved conjectures remind us that even the most basic mathematical concepts can hold surprising depths and lead to fascinating research questions. The exploration of unit fractions continues to offer a unique blend of historical insight and cutting-edge mathematical challenges, solidifying its place as a significant topic within the broader world of mathematics.
Latest Posts
Latest Posts
-
Is 20 A Multiple Of 10
Apr 01, 2025
-
What Are Rows In Periodic Table
Apr 01, 2025
-
Sound Waves Cannot Travel In A Vacuum Because
Apr 01, 2025
-
What Is The Difference Between Place And Value
Apr 01, 2025
-
What Is 15 Percent Of 200
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about A Fraction With Numerator 1 Is Called . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
