What Is Bigger 2 3 Or 1 2
Juapaving
May 10, 2025 · 5 min read
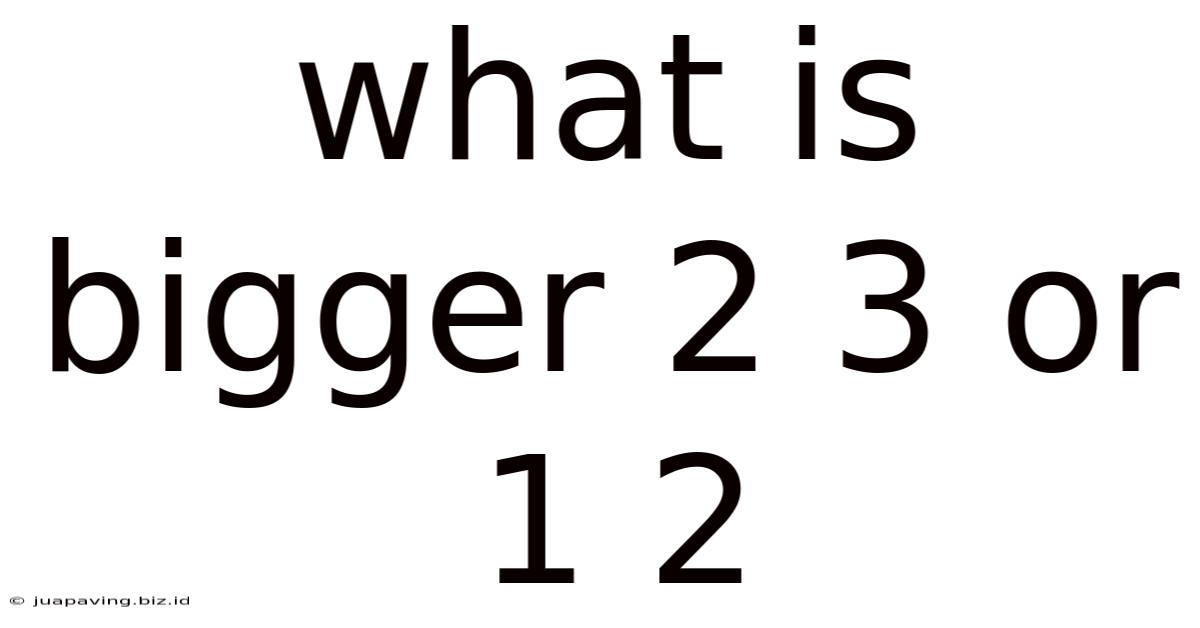
Table of Contents
What's Bigger: 2/3 or 1/2? A Deep Dive into Fraction Comparison
The seemingly simple question, "What's bigger: 2/3 or 1/2?", often trips up even adults. While the answer might seem immediately obvious to some, a deeper understanding of fractions is crucial for anyone working with numbers, whether it's in everyday life, academic pursuits, or professional fields. This article provides a comprehensive exploration of this seemingly basic comparison, delving into various methods to determine which fraction is larger, and highlighting the underlying mathematical concepts involved. We'll explore multiple approaches, ensuring a clear and thorough understanding for all readers.
Understanding Fractions: The Building Blocks
Before diving into the comparison, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 2/3, the numerator (2) tells us we have two parts, and the denominator (3) tells us the whole is divided into three equal parts.
Method 1: Visual Representation
One of the easiest ways to compare 2/3 and 1/2 is through visual representation. Imagine two identical circles or bars.
- Representing 1/2: Divide the first circle into two equal parts. Shade one part to represent 1/2.
- Representing 2/3: Divide the second circle into three equal parts. Shade two parts to represent 2/3.
By visually comparing the shaded areas, it becomes clear that the shaded area representing 2/3 is larger than the shaded area representing 1/2. This method is particularly helpful for beginners as it provides an intuitive understanding of fraction comparison.
Method 2: Finding a Common Denominator
A more mathematically rigorous method involves finding a common denominator for both fractions. This means finding a number that is divisible by both the denominators (3 and 2). The least common multiple (LCM) of 3 and 2 is 6.
- Converting 1/2: To convert 1/2 to a fraction with a denominator of 6, we multiply both the numerator and the denominator by 3: (1 x 3) / (2 x 3) = 3/6.
- Converting 2/3: To convert 2/3 to a fraction with a denominator of 6, we multiply both the numerator and the denominator by 2: (2 x 2) / (3 x 2) = 4/6.
Now, comparing 3/6 and 4/6 is straightforward. Since 4 > 3, we conclude that 4/6 (or 2/3) is larger than 3/6 (or 1/2). This method emphasizes the importance of equivalent fractions and provides a systematic approach to comparison.
Method 3: Decimal Conversion
Another effective method is to convert both fractions into their decimal equivalents.
- Converting 1/2: 1 ÷ 2 = 0.5
- Converting 2/3: 2 ÷ 3 ≈ 0.6667
Comparing 0.5 and 0.6667, it's clear that 0.6667 (or 2/3) is larger than 0.5 (or 1/2). This method leverages our familiarity with decimal numbers and provides a quick and accurate comparison, especially when dealing with more complex fractions.
Method 4: Cross-Multiplication
Cross-multiplication offers a concise and efficient method for comparing fractions. This method involves multiplying the numerator of one fraction by the denominator of the other and vice-versa.
- Cross-multiplying 2/3 and 1/2:
- 2 (numerator of 2/3) x 2 (denominator of 1/2) = 4
- 3 (denominator of 2/3) x 1 (numerator of 1/2) = 3
Since 4 > 3, we conclude that 2/3 is larger than 1/2. This method provides a shortcut for comparison, avoiding the need for common denominators or decimal conversions.
Beyond the Basics: Extending the Concept
While the comparison between 2/3 and 1/2 serves as a foundational example, the principles discussed here can be applied to more complex fractions. The key is to consistently apply the chosen method to ensure accurate results. For instance, when comparing fractions with larger numerators and denominators, finding the common denominator might become more computationally intensive. In such scenarios, decimal conversion or cross-multiplication can offer more efficient solutions.
Real-World Applications
Understanding fraction comparison extends far beyond the realm of mathematics textbooks. It finds practical applications in numerous real-world scenarios:
- Cooking and Baking: Recipes often require precise measurements, necessitating accurate fraction comparison to ensure the correct proportions of ingredients.
- Construction and Engineering: Precise measurements and calculations are critical in construction and engineering projects. Accurate fraction comparison is crucial for ensuring structural integrity and functionality.
- Finance and Budgeting: Managing finances and budgets often involves working with fractions and percentages, making fraction comparison an essential skill.
- Data Analysis: Data analysis often involves comparing fractions and proportions, requiring a strong grasp of fraction comparison techniques.
Addressing Common Mistakes and Misconceptions
While the comparison of 2/3 and 1/2 seems straightforward, several common misconceptions can lead to errors. Here are a few to watch out for:
- Focusing solely on numerators: It's crucial to remember that the denominator plays an equally important role. Simply comparing numerators without considering the denominators can lead to incorrect conclusions.
- Incorrect application of common denominator methods: Errors can arise from incorrect calculations when finding common denominators or converting fractions. Careful attention to detail is crucial.
- Misunderstanding decimal conversions: Rounding errors during decimal conversion can affect the accuracy of the comparison. It's important to maintain sufficient decimal places to ensure accuracy.
Conclusion: Mastering Fraction Comparison
The seemingly simple question of comparing 2/3 and 1/2 reveals a deeper understanding of fundamental mathematical concepts. Through various methods—visual representation, finding a common denominator, decimal conversion, and cross-multiplication—we’ve explored different approaches to determining which fraction is larger. By understanding these methods and avoiding common pitfalls, you can confidently compare fractions of any complexity, equipping you with a valuable skill applicable across various aspects of life. Remember that consistent practice and a solid grasp of the underlying concepts are key to mastering fraction comparison. This understanding will not only improve your mathematical skills but also enhance your problem-solving abilities in diverse real-world scenarios.
Latest Posts
Latest Posts
-
Negative Words That Start With K
May 10, 2025
-
What Are The Real Fourth Roots Of 256
May 10, 2025
-
Lcm Of 8 6 And 3
May 10, 2025
-
How Is Mitosis Different In Plant And Animal Cells
May 10, 2025
-
Positively Charged Particle In The Atom
May 10, 2025
Related Post
Thank you for visiting our website which covers about What Is Bigger 2 3 Or 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.