What Is All The Factors Of 33
Juapaving
Mar 28, 2025 · 5 min read
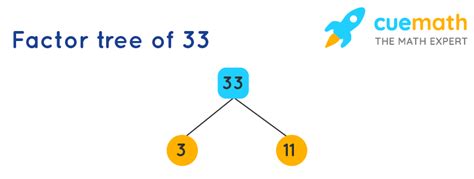
Table of Contents
What are all the factors of 33? A Deep Dive into Prime Factorization and Divisibility
Finding all the factors of a number might seem like a simple arithmetic task, but it opens a door to understanding fundamental concepts in number theory, like prime factorization and divisibility rules. Let's explore the factors of 33 in detail, examining the process, the underlying mathematical principles, and some related concepts.
Understanding Factors
A factor (or divisor) of a number is a whole number that divides the number exactly without leaving a remainder. In simpler terms, if you can divide a number by another number and get a whole number result, then the second number is a factor of the first.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. This is because 12 can be divided evenly by each of these numbers.
Finding the Factors of 33
Now, let's focus on the number 33. To find all its factors, we can employ a systematic approach:
-
Start with 1: Every number has 1 as a factor.
-
Check for prime factors: The next step is to check for prime numbers that divide 33. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. 33 is clearly divisible by 3 (3 x 11 = 33). 3 and 11 are both prime numbers.
-
Identify the pairs: Since 3 and 11 are prime factors and their product is 33, we've found two pairs of factors: 3 and 11, and their respective reciprocals in relation to 33: 33/3 = 11, and 33/11=3.
-
Include 1 and the number itself: Remember to include 1 and the number itself (33) as factors. Every number is divisible by 1 and itself.
Therefore, the factors of 33 are 1, 3, 11, and 33.
Prime Factorization: The Foundation
The process of finding the prime factors of a number is called prime factorization. It's a fundamental concept in number theory because every whole number greater than 1 can be expressed uniquely as a product of prime numbers (ignoring the order). This unique representation is known as the fundamental theorem of arithmetic.
In the case of 33, the prime factorization is simply 3 x 11. This means that 3 and 11 are the only prime numbers that, when multiplied together, equal 33.
Divisibility Rules: Shortcuts for Factor Identification
Understanding divisibility rules can help us quickly determine if a number is a factor of another. Here are some relevant divisibility rules:
- Divisibility by 1: Every number is divisible by 1.
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3. (3 + 3 = 6, which is divisible by 3, so 33 is divisible by 3).
- Divisibility by 11: A number is divisible by 11 if the alternating sum of its digits is divisible by 11. (3 - 3 = 0, which is divisible by 11, so 33 is divisible by 11).
These rules can save time when searching for factors, especially for larger numbers.
Visualizing Factors: Factor Trees
A factor tree is a visual tool to represent the prime factorization of a number. For 33, the factor tree would look like this:
33
/ \
3 11
This clearly shows that 3 and 11 are the prime factors of 33.
Applications of Factorization
Understanding factors and prime factorization isn't just an academic exercise; it has numerous applications in various fields:
-
Cryptography: Prime factorization is crucial in modern cryptography, particularly in algorithms like RSA, which rely on the difficulty of factoring large numbers into their prime components.
-
Modular Arithmetic: Factors play a key role in modular arithmetic, a branch of number theory used in computer science, coding theory, and cryptography.
-
Algebra: Factoring expressions in algebra relies on the same principles as factoring numbers, enabling simplification and solving equations.
-
Fraction Simplification: Finding the greatest common factor (GCF) of the numerator and denominator of a fraction allows for simplification. The GCF is the largest factor common to both numbers. For example, simplifying the fraction 33/66 involves finding the GCF of 33 and 66, which is 33. Simplifying the fraction gives 1/2.
-
Number Theory Research: The study of factors and prime numbers remains a vibrant area of mathematical research, with unsolved problems that continue to challenge mathematicians.
Exploring Related Concepts
Let's delve into some concepts closely related to factors:
-
Greatest Common Factor (GCF): The greatest common factor (GCF) of two or more numbers is the largest number that divides all the given numbers without leaving a remainder. For example, the GCF of 33 and 66 is 33.
-
Least Common Multiple (LCM): The least common multiple (LCM) of two or more numbers is the smallest number that is a multiple of all the given numbers. The LCM of 33 and 66 is 66.
-
Divisibility Tests: Knowing divisibility rules for various numbers can significantly speed up the process of factor identification.
-
Prime Numbers: Understanding prime numbers is essential for prime factorization, as prime numbers are the building blocks of all composite numbers (non-prime numbers). The infinitude of prime numbers is a fundamental theorem in number theory.
Conclusion: The Significance of Factors
The seemingly simple question of finding all the factors of 33 leads us on a journey into the fascinating world of number theory. From the fundamental theorem of arithmetic to the practical applications in various fields, understanding factors and prime factorization provides a solid foundation for mathematical exploration and problem-solving. The seemingly simple number 33, with its factors 1, 3, 11, and 33, acts as a gateway to deeper insights into the structure and behavior of numbers. Mastering this concept unlocks a world of possibilities in mathematics and beyond. By understanding the process and the underlying mathematical principles, one gains a stronger grasp of number theory and its applications. Remember to always utilize systematic approaches and efficient methods like divisibility rules and factor trees to streamline the identification of factors.
Latest Posts
Latest Posts
-
How Many Mm Are In One Meter
Mar 31, 2025
-
Does A Flatworm Have A Coelom
Mar 31, 2025
-
An Automobile Engine Converts Energy Into Energy
Mar 31, 2025
-
Is Chlorine A Metal Nonmetal Or Metalloid
Mar 31, 2025
-
Which Of The Following Is A Compound
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is All The Factors Of 33 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
