What Is A Rectangle Model In Math
Juapaving
Mar 30, 2025 · 5 min read
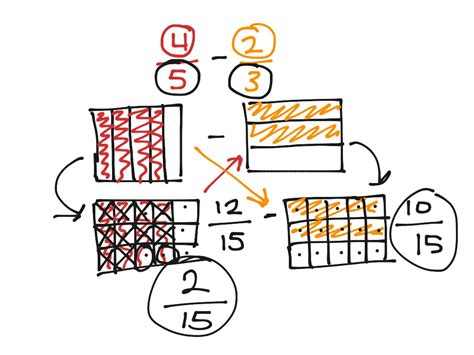
Table of Contents
What is a Rectangular Model in Math? A Comprehensive Guide
The rectangular model, also known as the area model, is a powerful visual tool used in mathematics to represent and solve various problems, particularly those involving multiplication, division, factoring, and algebraic manipulations. Its versatility extends across different grade levels, from elementary school multiplication to advanced algebraic concepts. This comprehensive guide delves into the intricacies of rectangular models, exploring their applications, benefits, and the underlying mathematical principles they represent.
Understanding the Basics: Visualizing Multiplication
At its core, the rectangular model leverages the fundamental concept that the area of a rectangle is calculated by multiplying its length and width. This simple geometric relationship provides a visual framework for understanding multiplication, making it more intuitive and less abstract for learners.
Representing Multiplication: A Simple Example
Consider the multiplication problem 12 x 7. Instead of relying solely on rote memorization or standard algorithms, we can use a rectangular model to visualize the solution.
-
Draw a rectangle: Draw a rectangle and divide it into smaller rectangles to represent the factors. For 12 x 7, you could divide the rectangle into 12 columns (representing the factor 12) and 7 rows (representing the factor 7).
-
Partition the rectangle: You can further subdivide the rectangle. For instance, you could break the 12 columns into 10 columns and 2 columns. This partitioning simplifies the calculations.
-
Calculate the area of smaller rectangles: Now, calculate the area of each smaller rectangle. You'll have three smaller rectangles:
- A 10 x 7 rectangle with an area of 70.
- A 2 x 7 rectangle with an area of 14.
-
Add the areas: Finally, add the areas of the smaller rectangles: 70 + 14 = 84. Therefore, 12 x 7 = 84.
This visual approach helps students understand the distributive property of multiplication (a(b + c) = ab + ac) because they directly see how the area of the larger rectangle is the sum of the areas of the smaller rectangles.
Beyond Basic Multiplication: Advanced Applications
The rectangular model's usefulness extends far beyond elementary multiplication. Its versatility makes it an invaluable tool in various mathematical contexts:
1. Multiplication of Larger Numbers:
The same principles apply to multiplying larger numbers. For example, consider 23 x 15. The rectangle can be partitioned into four smaller rectangles representing (20 x 10), (20 x 5), (3 x 10), and (3 x 5). Calculating and summing the areas of these smaller rectangles provides the final product.
2. Multiplication of Polynomials:
The rectangular model is extremely useful in algebra when multiplying polynomials. Imagine multiplying (x + 2) and (x + 3). We can create a rectangle where one side represents (x + 2) and the other represents (x + 3).
The rectangle is then divided into four smaller rectangles:
- x * x = x²
- x * 2 = 2x
- x * 3 = 3x
- 2 * 3 = 6
The product (x + 2)(x + 3) is obtained by summing the areas: x² + 2x + 3x + 6 = x² + 5x + 6.
3. Factoring Polynomials:
The area model can be used in reverse to factor polynomials. Given a polynomial like x² + 5x + 6, you can construct a rectangle where the total area is represented by the polynomial. You then determine the dimensions of the rectangle by finding factors whose product equals the constant term (6) and whose sum equals the coefficient of the linear term (5). This leads to factoring the polynomial as (x + 2)(x + 3).
4. Solving Division Problems:
The rectangular model aids in understanding division by representing the dividend as the area of a rectangle and one of the factors (the divisor) as one of the dimensions. Then, the other dimension represents the quotient. For instance, to divide 84 by 12, you would create a rectangle with an area of 84 and one side of 12; the other side would represent the quotient (7).
5. Understanding Fractions and Decimals:
Rectangular models can effectively illustrate operations with fractions and decimals. For instance, multiplying fractions can be visualized by dividing a rectangle into parts that represent the fractions involved. Similarly, understanding decimal multiplication and division becomes more intuitive when using the area model.
Benefits of Using Rectangular Models
The rectangular model offers several significant advantages over traditional methods:
-
Visual Representation: It provides a concrete visual representation of abstract mathematical concepts, making them more accessible and understandable, especially for visual learners.
-
Improved Conceptual Understanding: By physically manipulating the model, students develop a deeper understanding of the underlying mathematical principles rather than simply memorizing procedures.
-
Enhanced Problem-Solving Skills: The model encourages strategic thinking and problem-solving skills as students must determine how to partition the rectangle effectively to simplify calculations.
-
Increased Engagement and Motivation: The hands-on nature of the rectangular model increases student engagement and motivation compared to purely symbolic manipulations.
-
Versatile Application: Its versatility allows it to be used across various mathematical topics, enhancing coherence and connections between different concepts.
-
Bridging Concrete and Abstract: It bridges the gap between concrete manipulatives and abstract symbolic representations, making the transition smoother for students.
Addressing Potential Challenges
While the rectangular model offers numerous benefits, some challenges may arise:
-
Initial Complexity: The initial learning curve might seem steep for students unfamiliar with the method, requiring careful introduction and guided practice.
-
Spatial Reasoning: Students may require development in spatial reasoning skills to effectively partition rectangles and interpret the visual representations.
-
Larger Numbers and Variables: Using the model with very large numbers or complex algebraic expressions can become cumbersome and less efficient than algorithmic approaches.
However, these challenges are often outweighed by the significant benefits of enhanced understanding and problem-solving skills.
Conclusion: A Powerful Tool for Mathematical Understanding
The rectangular model stands as a powerful and versatile tool in mathematics education. Its ability to visualize abstract concepts, improve conceptual understanding, and enhance problem-solving skills makes it an invaluable resource for students at various grade levels. While requiring initial instruction and practice, its benefits, from simplifying multiplication to facilitating understanding of polynomial manipulation, justify its continued use in enhancing mathematical literacy and achievement. By fostering a deeper grasp of underlying principles rather than rote memorization, the rectangular model empowers students to become more confident and proficient mathematicians. Its adaptability across various mathematical domains highlights its enduring relevance and significance in the learning process.
Latest Posts
Latest Posts
-
5 Letter Words Starting With A S
Apr 01, 2025
-
How Many Atp Does The Electron Transport Chain Produce
Apr 01, 2025
-
When Do You Use Left Hand Rule Electromagnetism
Apr 01, 2025
-
All Of The Chemical Reactions Of The Cell Are Called
Apr 01, 2025
-
Is Pressure Directly Proportional To Temperature
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is A Rectangle Model In Math . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
