What Is A Multiple Of 42
Juapaving
Mar 31, 2025 · 6 min read
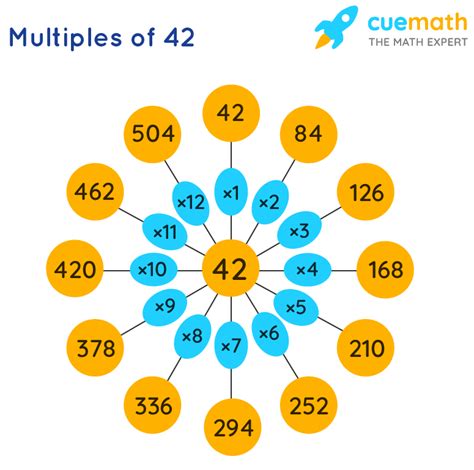
Table of Contents
What is a Multiple of 42? A Deep Dive into Multiplication and Divisibility
Understanding multiples is a fundamental concept in mathematics, crucial for various applications from basic arithmetic to advanced algebra. This comprehensive guide delves into the concept of multiples, focusing specifically on multiples of 42. We'll explore what multiples are, how to identify them, their properties, and practical applications. We'll also touch upon related mathematical concepts to provide a holistic understanding.
Understanding Multiples
A multiple of a number is the product of that number and any integer (whole number). In simpler terms, it's the result you get when you multiply a number by another whole number. For example:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, and so on.
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, and so on.
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, and so on.
Notice that multiples always include the original number itself (e.g., 2 is a multiple of 2). Also, the multiples of a given number extend infinitely in both positive and negative directions. However, we often focus on positive multiples in practical applications.
Identifying Multiples of 42
Now, let's focus on the number 42. A multiple of 42 is any number that results from multiplying 42 by an integer. To find multiples of 42, we simply multiply 42 by different integers:
- 42 x 1 = 42 (The first multiple of 42)
- 42 x 2 = 84 (The second multiple of 42)
- 42 x 3 = 126 (The third multiple of 42)
- 42 x 4 = 168 (The fourth multiple of 42)
- 42 x 5 = 210 (The fifth multiple of 42)
- And so on...
We can continue this process indefinitely. The sequence of multiples of 42 is: 42, 84, 126, 168, 210, 252, 294, 336, 378, 420, and so forth.
Finding Multiples Using a Calculator or Spreadsheet
For larger multiples, using a calculator or a spreadsheet program can be incredibly helpful. Simply input the formula 42 * n, where 'n' represents the integer you're multiplying by. Spreadsheets, in particular, allow you to easily generate a long sequence of multiples by dragging the formula down.
Properties of Multiples of 42
Multiples of 42 share several interesting properties:
- Divisibility: All multiples of 42 are divisible by 42 without leaving a remainder. This is the defining characteristic of a multiple.
- Factors: The prime factorization of 42 is 2 x 3 x 7. Therefore, all multiples of 42 will also contain these prime factors. This is a crucial concept in number theory and has implications in cryptography and other fields.
- Even Numbers: All multiples of 42 are even numbers because 42 itself is an even number (it's divisible by 2). This is because the product of an even number and any integer will always be even.
- Arithmetic Sequence: The sequence of multiples of 42 forms an arithmetic progression. This means the difference between consecutive multiples is constant (in this case, 42).
Applications of Multiples
Understanding multiples has practical applications in numerous areas:
- Measurement: Multiples are used in measuring quantities. For instance, multiples of 42 could represent distances, weights, or volumes depending on the units used. If a certain task requires 42 units of work, then multiples of 42 would signify completing multiple instances of that task.
- Scheduling: Multiples can assist in scheduling events that repeat at regular intervals. For example, if a certain event occurs every 42 days, understanding multiples helps determine future occurrences.
- Inventory Management: Businesses use multiples to manage inventory. If a product is packed in boxes of 42 units, then multiples of 42 would represent the total number of units in stock.
- Pattern Recognition: In fields like computer science and mathematics, identifying patterns often involves recognizing sequences that are multiples of a specific number.
- Number Theory: The study of multiples forms a cornerstone of number theory, a branch of mathematics with applications in cryptography, coding theory, and other advanced areas.
Distinguishing between Multiples, Factors, and Divisors
It's important to distinguish between multiples, factors, and divisors. While related, they represent different aspects of number relationships:
- Multiples: The numbers obtained by multiplying a given number by an integer (e.g., multiples of 42 are 42, 84, 126...).
- Factors (or Divisors): The numbers that divide a given number without leaving a remainder (e.g., factors of 42 are 1, 2, 3, 6, 7, 14, 21, 42).
A number is a multiple of another if the second number is a factor (or divisor) of the first. For example, 84 is a multiple of 42, and 42 is a factor (divisor) of 84.
Finding the Least Common Multiple (LCM) and Greatest Common Divisor (GCD)
The concepts of LCM and GCD are closely related to multiples and factors. Let's define them:
- Least Common Multiple (LCM): The smallest positive number that is a multiple of two or more given numbers. For example, the LCM of 42 and 60 is 420.
- Greatest Common Divisor (GCD): The largest positive integer that divides each of the given integers without leaving a remainder. For example, the GCD of 42 and 60 is 6.
Calculating the LCM and GCD can be done using various methods, including prime factorization and the Euclidean algorithm. These concepts have significant applications in various mathematical problems and in areas like cryptography.
Advanced Concepts Related to Multiples of 42
While the basic concept of multiples is straightforward, delving deeper unveils connections to more advanced mathematical ideas:
- Modular Arithmetic: Modular arithmetic involves working with remainders after division. Understanding multiples is crucial for understanding congruence relations in modular arithmetic. For instance, we can say that 126 is congruent to 0 (mod 42), meaning that 126 leaves a remainder of 0 when divided by 42.
- Number Theory: As previously mentioned, multiples play a vital role in number theory, a branch of mathematics dealing with the properties of integers. Concepts like prime factorization, divisibility rules, and the distribution of prime numbers are all intricately linked to the idea of multiples.
- Abstract Algebra: In abstract algebra, the concept of multiples is generalized to structures like groups and rings. This opens up connections to areas like group theory and ring theory.
Conclusion: The Enduring Importance of Multiples
The concept of multiples, seemingly simple at first glance, holds a foundational position in mathematics and numerous related fields. Understanding multiples of 42, or any number for that matter, is not merely an exercise in rote memorization but a key to unlocking deeper insights into the structure and patterns within numbers. From basic arithmetic problems to sophisticated mathematical theories, the principles of divisibility, factorization, and the properties of multiples provide a framework for tackling a wide array of challenges. The exploration of multiples extends far beyond the initial definition, offering a glimpse into the rich and multifaceted world of mathematical concepts. This understanding provides not only a firm foundation for mathematical proficiency but also equips individuals with a valuable toolset for practical applications across diverse disciplines.
Latest Posts
Latest Posts
-
How To Find A Supplementary Angle
Apr 02, 2025
-
How Can The Strength Of An Electromagnet Be Increased
Apr 02, 2025
-
If Qt Is Perpendicular To Pr
Apr 02, 2025
-
Which Base Is Not Present In Rna
Apr 02, 2025
-
What Is The Lcm Of 5 And 10
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is A Multiple Of 42 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
