What Is A Factor Of 63
Juapaving
Mar 30, 2025 · 5 min read
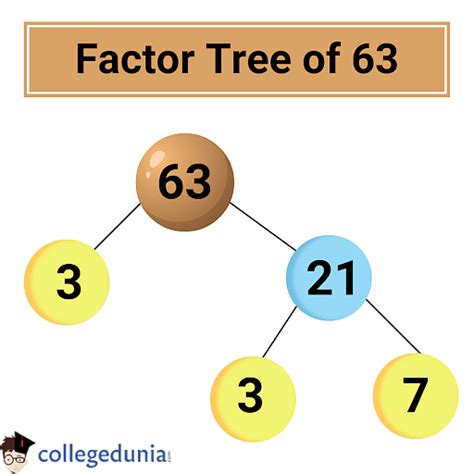
Table of Contents
What is a Factor of 63? A Deep Dive into Number Theory
Finding the factors of a number might seem like a simple arithmetic exercise, but it opens a door to a fascinating world of number theory with implications in various fields like cryptography and computer science. This comprehensive guide explores the concept of factors, focusing specifically on the factors of 63, and delving into related mathematical concepts.
Understanding Factors
A factor (or divisor) of a number is a whole number that divides the number exactly without leaving a remainder. In simpler terms, if you can divide a number by another number and get a whole number as the result, then the number you divided by is a factor.
For example, let's consider the number 12. Its factors are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 without leaving a remainder.
Finding the Factors of 63
To find the factors of 63, we systematically check which whole numbers divide 63 evenly. We can start by considering the smallest whole numbers:
- 1: 63 ÷ 1 = 63 (1 is a factor)
- 2: 63 ÷ 2 = 31.5 (2 is not a factor)
- 3: 63 ÷ 3 = 21 (3 is a factor)
- 4: 63 ÷ 4 = 15.75 (4 is not a factor)
- 5: 63 ÷ 5 = 12.6 (5 is not a factor)
- 6: 63 ÷ 6 = 10.5 (6 is not a factor)
- 7: 63 ÷ 7 = 9 (7 is a factor)
- 8: 63 ÷ 8 = 7.875 (8 is not a factor)
- 9: 63 ÷ 9 = 7 (9 is a factor)
Notice that after 9, we start encountering numbers we've already seen (their quotients will be numbers less than 9). This is a pattern we can leverage. Once we reach the square root of the number (√63 ≈ 7.9), we only need to check numbers up to this point, as the remaining factors will be their corresponding pairs.
Therefore, the factors of 63 are 1, 3, 7, 9, 21, and 63.
Prime Factorization and Factors of 63
Prime factorization is a powerful tool for finding all the factors of a number. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11, etc.). Prime factorization involves expressing a number as a product of its prime factors.
To find the prime factorization of 63:
- We start by dividing 63 by the smallest prime number, 2. Since 63 is odd, 2 is not a factor.
- Next, we try the next prime number, 3. 63 ÷ 3 = 21.
- Now we have 3 × 21. 21 is not a prime number, so we continue factoring. 21 ÷ 3 = 7.
- Now we have 3 × 3 × 7. Both 3 and 7 are prime numbers.
Therefore, the prime factorization of 63 is 3² × 7.
Knowing the prime factorization allows us to easily find all the factors. We simply combine the prime factors in various ways:
- 3⁰ × 7⁰ = 1
- 3¹ × 7⁰ = 3
- 3² × 7⁰ = 9
- 3⁰ × 7¹ = 7
- 3¹ × 7¹ = 21
- 3² × 7¹ = 63
This method systematically generates all the factors without missing any.
Factors and Divisibility Rules
Understanding divisibility rules can significantly speed up the process of finding factors. These rules help determine if a number is divisible by a specific number without performing the actual division.
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3. (6 + 3 = 9, which is divisible by 3, so 63 is divisible by 3)
- Divisibility by 7: There isn't a simple divisibility rule for 7 as there are for some other numbers. However, we can use division to check for divisibility by 7.
- Divisibility by 9: A number is divisible by 9 if the sum of its digits is divisible by 9. (6 + 3 = 9, which is divisible by 9, so 63 is divisible by 9)
Factors and Their Applications
The concept of factors has wide-ranging applications in various fields:
1. Cryptography:
Prime factorization plays a crucial role in modern cryptography, particularly in RSA encryption. The security of RSA relies on the difficulty of factoring large numbers into their prime factors.
2. Computer Science:
Understanding factors is essential in algorithm design and optimization. Many algorithms involve iterative processes that depend on the factors of numbers for efficient execution.
3. Number Theory:
Factorization is a fundamental concept in number theory, leading to the exploration of prime numbers, perfect numbers, amicable numbers, and many other fascinating mathematical topics.
Beyond the Basics: Greatest Common Factor (GCF) and Least Common Multiple (LCM)
Two important concepts closely related to factors are the Greatest Common Factor (GCF) and the Least Common Multiple (LCM).
-
Greatest Common Factor (GCF): The GCF of two or more numbers is the largest number that divides all of them without leaving a remainder. For instance, the GCF of 12 and 18 is 6.
-
Least Common Multiple (LCM): The LCM of two or more numbers is the smallest number that is a multiple of all the numbers. For example, the LCM of 12 and 18 is 36.
Finding the GCF and LCM is often done using prime factorization. For example, to find the GCF of 63 and 42:
- Prime factorization of 63: 3² × 7
- Prime factorization of 42: 2 × 3 × 7
The GCF is found by taking the lowest power of each common prime factor: 3¹ × 7¹ = 21. The GCF of 63 and 42 is 21.
To find the LCM, we take the highest power of each prime factor present in either factorization: 2¹ × 3² × 7¹ = 126. The LCM of 63 and 42 is 126.
Conclusion
Understanding factors, particularly the factors of a number like 63, provides a foundation for exploring various branches of mathematics and their applications. From the simple act of dividing to the complexities of cryptography and algorithm design, the concept of factors proves to be essential and far-reaching. By mastering the techniques of finding factors, using prime factorization, and applying divisibility rules, you'll open up a world of mathematical exploration and practical applications. Further exploration into concepts like GCF and LCM will further solidify your understanding and expand your mathematical toolkit.
Latest Posts
Latest Posts
-
Is Na2s An Acid Or Base
Apr 01, 2025
-
Sum Of First 10 Prime Numbers
Apr 01, 2025
-
Why Is The Amazon Called The Lungs Of The Earth
Apr 01, 2025
-
A Rectangle With Four Equal Sides
Apr 01, 2025
-
Which Elements Had A Filled Outermost Shell
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is A Factor Of 63 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
