What Is A Factor Of 180
Juapaving
Mar 28, 2025 · 6 min read
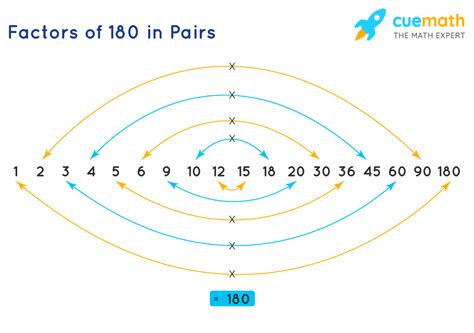
Table of Contents
What is a Factor of 180? A Deep Dive into Number Theory
Finding the factors of a number might seem like a simple arithmetic task, but understanding the concept opens doors to a fascinating world of number theory. This article delves into the question, "What is a factor of 180?", exploring various methods to identify them, their significance in mathematics, and their applications in real-world problems. We'll go beyond simply listing the factors and explore the underlying mathematical principles.
Understanding Factors and Divisibility
Before we tackle the factors of 180, let's establish a clear understanding of what a factor is. A factor (also known as a divisor) of a number is an integer that divides the number exactly without leaving a remainder. In other words, if 'a' is a factor of 'b', then b/a results in a whole number.
Divisibility is the concept of one number being divisible by another. If a number 'b' is divisible by another number 'a', it means that 'a' is a factor of 'b'. For example, 180 is divisible by 10, meaning 10 is a factor of 180.
Finding the Factors of 180: Multiple Approaches
There are several ways to determine the factors of 180. Let's explore some of the most common and effective methods:
1. The Factor Pair Method
This method involves systematically identifying pairs of numbers that multiply to 180. We start with 1, which is always a factor of any number, and its corresponding pair:
- 1 x 180 = 180
- 2 x 90 = 180
- 3 x 60 = 180
- 4 x 45 = 180
- 5 x 36 = 180
- 6 x 30 = 180
- 9 x 20 = 180
- 10 x 18 = 180
- 12 x 15 = 180
Notice that after 12, we start to repeat factor pairs (in reverse order). This is because we've essentially found all the factors.
Therefore, the factors of 180 are: 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, and 180.
2. Prime Factorization
Prime factorization is a powerful technique that breaks down a number into its prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11...). The prime factorization of 180 is:
180 = 2² x 3² x 5
This means 180 is composed of two 2's, two 3's, and one 5. To find all factors, we consider all possible combinations of these prime factors:
- 2⁰ x 3⁰ x 5⁰ = 1
- 2¹ x 3⁰ x 5⁰ = 2
- 2² x 3⁰ x 5⁰ = 4
- 2⁰ x 3¹ x 5⁰ = 3
- 2¹ x 3¹ x 5⁰ = 6
- 2² x 3¹ x 5⁰ = 12
- 2⁰ x 3² x 5⁰ = 9
- 2¹ x 3² x 5⁰ = 18
- 2² x 3² x 5⁰ = 36
- 2⁰ x 3⁰ x 5¹ = 5
- 2¹ x 3⁰ x 5¹ = 10
- 2² x 3⁰ x 5¹ = 20
- 2⁰ x 3¹ x 5¹ = 15
- 2¹ x 3¹ x 5¹ = 30
- 2² x 3¹ x 5¹ = 60
- 2⁰ x 3² x 5¹ = 45
- 2¹ x 3² x 5¹ = 90
- 2² x 3² x 5¹ = 180
This method systematically generates all possible factors, confirming our list from the factor pair method.
3. Using Division
We can also find factors by systematically dividing 180 by integers starting from 1. If the division results in a whole number, that integer is a factor. We continue this process until the quotient becomes less than the divisor.
The Significance of Factors in Mathematics
Factors are fundamental to many areas of mathematics:
-
Greatest Common Factor (GCF): The GCF of two or more numbers is the largest number that divides all of them without leaving a remainder. Finding the GCF is crucial in simplifying fractions and solving various mathematical problems. For example, the GCF of 180 and 270 is 90.
-
Least Common Multiple (LCM): The LCM of two or more numbers is the smallest number that is a multiple of all of them. LCMs are essential in working with fractions, particularly when adding or subtracting them. The LCM of 180 and 270 is 540.
-
Divisibility Rules: Understanding factors helps us apply divisibility rules, which are shortcuts to determine if a number is divisible by another number without performing long division. For example, a number is divisible by 3 if the sum of its digits is divisible by 3; 1+8+0 = 9, which is divisible by 3, so 180 is divisible by 3.
Real-World Applications of Factors
The concept of factors extends far beyond the realm of abstract mathematics. It finds practical applications in various fields:
-
Geometry: Factors are used in calculating areas and volumes of shapes. For instance, if you're designing a rectangular garden with an area of 180 square feet, you'd need to consider the various factor pairs to determine possible dimensions.
-
Measurement and Conversion: Converting units of measurement often involves working with factors. For example, converting inches to feet or liters to gallons involves using conversion factors.
-
Data Organization and Arrangement: Factors play a role in arranging data in grids or arrays. For instance, if you have 180 items to arrange in a rectangular grid, you'd need to consider the factors of 180 to determine the possible arrangements.
-
Scheduling and Time Management: Factors can help in scheduling tasks or events. For instance, if a task takes 180 minutes to complete and you want to break it down into equal intervals, the factors of 180 will determine the possible durations of these intervals.
-
Computer Science: In computer programming, factors are used in algorithms related to number theory, cryptography, and optimization.
Beyond the Basics: Exploring Further
The exploration of factors goes far beyond simply identifying them for a single number. Advanced concepts include:
-
Number of Divisors: The number of divisors a number has is related to its prime factorization. The number of divisors of 180 can be calculated using the exponents in its prime factorization (2² x 3² x 5¹). The calculation is (2+1)(2+1)(1+1) = 18. Therefore, 180 has 18 divisors.
-
Perfect Numbers: A perfect number is a positive integer that is equal to the sum of its proper divisors (excluding the number itself). 6 is a perfect number (1 + 2 + 3 = 6). While 180 is not a perfect number, understanding perfect numbers provides insight into the intricate relationships between numbers and their divisors.
-
Abundant and Deficient Numbers: A number is abundant if the sum of its proper divisors is greater than the number itself, and deficient if the sum is less than the number itself. 180 is an abundant number.
Conclusion: Factors – A Foundation of Number Theory
Understanding factors is essential for mastering various mathematical concepts and solving real-world problems. This exploration of the factors of 180 has demonstrated multiple approaches to identify them, highlighting their significance in number theory and showcasing their applicability in diverse fields. The seemingly simple question, "What is a factor of 180?" unveils a deeper appreciation for the elegance and practicality of number theory. From finding the greatest common factor to understanding prime factorization, the ability to work with factors provides a solid foundation for further mathematical exploration. The journey into the world of numbers, beginning with a seemingly simple concept like factors, is an endlessly fascinating and rewarding one.
Latest Posts
Latest Posts
-
5 Letter Word That Starts With Vi
Mar 31, 2025
-
Can Acquired Characteristics Be Passed On The Next Generation
Mar 31, 2025
-
What Are The Three Body Parts Of A Mollusk
Mar 31, 2025
-
How Many Feet Is 45 Inches
Mar 31, 2025
-
Is The Square Root Of 12 Rational Or Irrational
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is A Factor Of 180 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
