What Is A Common Multiple Of 3 4 And 5
Juapaving
Mar 28, 2025 · 5 min read
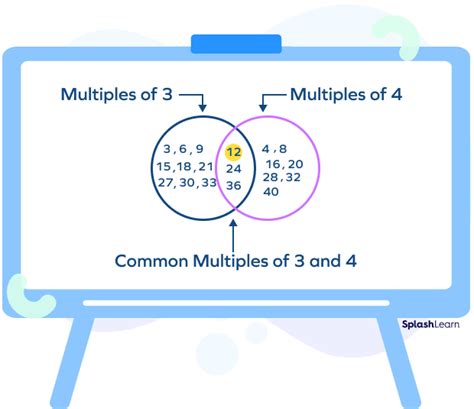
Table of Contents
What is the Least Common Multiple (LCM) of 3, 4, and 5? A Deep Dive into Finding Common Multiples
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with applications ranging from simple scheduling problems to complex engineering calculations. This article will explore the various methods to determine the LCM of 3, 4, and 5, delve into the underlying mathematical principles, and show you how this seemingly simple problem can reveal deeper mathematical insights.
Understanding Least Common Multiples (LCM)
Before we tackle the specific problem of finding the LCM of 3, 4, and 5, let's establish a solid understanding of what a least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12... The multiples of 3 are 3, 6, 9, 12, 15... The common multiples of 2 and 3 are 6, 12, 18... The smallest of these common multiples is 6, therefore, the LCM(2, 3) = 6.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60...
By examining these lists, we can see that the smallest number that appears in all three lists is 60. Therefore, the LCM(3, 4, 5) = 60.
While this method is intuitive and easy to understand, it becomes less practical as the numbers get larger. Imagine trying this method with numbers like 12, 24, and 36 – the list of multiples would grow considerably.
Method 2: Prime Factorization
This method provides a more efficient and systematic approach to finding the LCM, especially for larger numbers. It involves breaking down each number into its prime factors.
Step 1: Prime Factorization:
- 3 = 3¹
- 4 = 2²
- 5 = 5¹
Step 2: Identify the Highest Power of Each Prime Factor:
Looking at the prime factorizations above, we identify the highest power of each prime factor present:
- Highest power of 2: 2² = 4
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
Step 3: Multiply the Highest Powers:
To find the LCM, multiply these highest powers together:
LCM(3, 4, 5) = 2² * 3 * 5 = 4 * 3 * 5 = 60
This method is significantly more efficient than listing multiples, especially when dealing with larger numbers or a greater number of integers. It avoids the potentially lengthy process of generating and comparing large lists of multiples.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) are closely related. There's a formula that connects them:
LCM(a, b) * GCD(a, b) = a * b
This relationship can be extended to more than two numbers, although the calculations become more complex. While this method isn't the most direct for finding the LCM of 3, 4, and 5, it showcases a valuable mathematical connection between LCM and GCD.
First, let's find the GCD of 3, 4, and 5. The GCD is 1, as 3, 4, and 5 share no common divisors other than 1. However, extending the GCD formula to three numbers directly is not straightforward, and this method isn't as efficient as prime factorization in this case.
Applications of Finding the LCM
Understanding LCM has practical implications in various areas:
-
Scheduling: Imagine you have three events: one happens every 3 days, one every 4 days, and one every 5 days. To determine when all three events will coincide, you need to find the LCM(3, 4, 5) = 60. All three events will happen together every 60 days.
-
Fraction Arithmetic: Finding the LCM is crucial when adding or subtracting fractions with different denominators. You need to find the LCM of the denominators to find a common denominator.
-
Music Theory: LCMs are used in music theory to determine the least common period of rhythms.
-
Engineering: In areas like gear ratios and timing mechanisms, LCM is used to synchronize various components.
-
Computer Science: LCM is used in algorithms related to scheduling, concurrency, and synchronization.
Exploring Further: Beyond 3, 4, and 5
The methods discussed above can be applied to find the LCM of any set of integers. However, the complexity might increase with the number of integers involved or if the integers are large. For more complex scenarios, algorithms and software tools can be utilized for efficient computation.
Conclusion: The Significance of the LCM(3, 4, 5) = 60
The seemingly simple problem of finding the LCM of 3, 4, and 5—resulting in 60—demonstrates the fundamental importance of understanding least common multiples. This article explored various methods to solve this problem, highlighting the efficiency of prime factorization for larger numbers. Moreover, it emphasizes the widespread applications of LCM in diverse fields, from everyday scheduling to advanced engineering and computer science. Mastering the concept of LCM opens the door to a deeper understanding of mathematical principles and their practical applications in the real world. Understanding these foundational mathematical concepts provides a robust groundwork for more advanced mathematical studies and problem-solving skills. Therefore, the calculation of LCM(3, 4, 5) = 60 is not just a mathematical result but a stepping stone towards a broader comprehension of mathematical relationships and their utility in diverse fields.
Latest Posts
Latest Posts
-
72 As Product Of Prime Factors
Mar 31, 2025
-
How Many Valence Electrons Does S2 Have
Mar 31, 2025
-
What Is 17 25 As A Decimal
Mar 31, 2025
-
Region With The Lowest Atmospheric Pressure
Mar 31, 2025
-
Find The Prime Factorization Of 63
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is A Common Multiple Of 3 4 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
