Find The Prime Factorization Of 63
Juapaving
Mar 31, 2025 · 6 min read
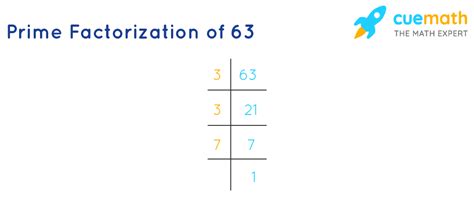
Table of Contents
Finding the Prime Factorization of 63: A Deep Dive into Number Theory
Finding the prime factorization of a number might seem like a simple task, especially with a smaller number like 63. However, understanding the process behind prime factorization unlocks a deeper understanding of number theory and its applications in various fields like cryptography and computer science. This article will not only show you how to find the prime factorization of 63 but will also delve into the underlying concepts, explore different methods, and highlight the significance of prime numbers in mathematics.
What is Prime Factorization?
Prime factorization is the process of breaking down a composite number (a number greater than 1 that is not prime) into its prime factors. A prime number is a natural number greater than 1 that has only two distinct positive divisors: 1 and itself. For example, 2, 3, 5, 7, 11, and 13 are prime numbers. The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers, disregarding the order of the factors. This uniqueness is crucial in many mathematical applications.
Method 1: The Factor Tree Method
The factor tree is a visual method that's particularly helpful for beginners. It's an iterative process where we repeatedly break down a number into smaller factors until we only have prime numbers remaining.
Let's find the prime factorization of 63 using the factor tree method:
-
Start with 63: We need to find two numbers that multiply to give 63. A convenient pair is 7 and 9.
-
Branch out: We draw two branches from 63, one leading to 7 and the other to 9.
-
Continue branching: 7 is a prime number, so we stop branching from that branch. However, 9 is not prime; it can be factored into 3 x 3. We branch from 9 to two 3s.
-
Identify the prime factors: Our factor tree ends with the prime numbers 3, 3, and 7.
Therefore, the prime factorization of 63 is 3 x 3 x 7, or 3² x 7.
63
/ \
7 9
/ \
3 3
Method 2: Repeated Division by Prime Numbers
This method is more systematic and suitable for larger numbers. We start by dividing the number by the smallest prime number (2), and if it's not divisible, we move on to the next prime number (3), and so on. We continue this process until the quotient is 1.
Let's find the prime factorization of 63 using repeated division:
-
Start with 63: 63 is not divisible by 2.
-
Divide by 3: 63 ÷ 3 = 21.
-
Divide by 3 again: 21 ÷ 3 = 7.
-
Divide by 7: 7 ÷ 7 = 1.
We have successfully divided 63 down to 1 using only prime numbers (3, 3, and 7). Therefore, the prime factorization of 63 is 3 x 3 x 7, or 3² x 7.
Understanding the Significance of Prime Factorization
The prime factorization of a number might seem like a simple mathematical exercise, but its applications extend far beyond basic arithmetic. Here are some key areas where it plays a vital role:
1. Cryptography
Prime numbers are the cornerstone of many modern encryption methods. RSA cryptography, widely used to secure online transactions, relies heavily on the difficulty of factoring very large numbers into their prime factors. The security of RSA lies in the computational infeasibility of factoring extremely large composite numbers (products of two very large prime numbers) in a reasonable amount of time.
2. Number Theory
Prime factorization is fundamental to numerous theorems and concepts in number theory, such as the distribution of prime numbers, the Riemann hypothesis (one of the most important unsolved problems in mathematics), and the study of modular arithmetic.
3. Computer Science
Algorithms for factoring numbers are crucial in computer science. Efficient algorithms for prime factorization are essential for tasks like cryptography, database management, and code optimization. The complexity of these algorithms influences the efficiency and security of various computational processes.
4. Other Applications
Prime factorization also finds applications in other areas, including:
- Coding Theory: Prime numbers play a role in designing error-correcting codes.
- Abstract Algebra: Prime factorization is used in various algebraic structures like rings and fields.
- Combinatorics: Prime numbers are involved in certain counting problems.
Advanced Techniques for Prime Factorization (for larger numbers)
While the factor tree and repeated division methods work well for smaller numbers like 63, they become less efficient for larger numbers. For very large numbers, more sophisticated algorithms are necessary:
- Trial Division: This is a basic algorithm that systematically checks for divisibility by prime numbers up to the square root of the number. While straightforward, it's computationally expensive for very large numbers.
- Sieve of Eratosthenes: This algorithm is efficient for finding all prime numbers up to a specified limit. It can be used as a pre-processing step for other factorization algorithms.
- Pollard's rho algorithm: This probabilistic algorithm is significantly faster than trial division for large composite numbers.
- General Number Field Sieve (GNFS): This is currently the most efficient known algorithm for factoring extremely large numbers. It's used for breaking cryptographic systems that rely on the difficulty of factoring large numbers.
Practical Applications of Prime Factorization: A Real-World Example
Let's consider a simplified example of how prime factorization can be applied in a real-world scenario. Imagine an online store needs to secure its payment gateway. They use RSA encryption, which relies on the product of two very large prime numbers (let's call them 'p' and 'q'). The product 'n = p x q' is publicly known, but the individual prime factors 'p' and 'q' are kept secret. Anyone trying to intercept the transaction would need to factor 'n' to obtain 'p' and 'q', but the sheer size of 'n' (potentially hundreds of digits) makes this computationally infeasible using current technology, ensuring the security of the transaction.
Conclusion: The Enduring Importance of Prime Numbers
The seemingly simple task of finding the prime factorization of 63 reveals a much deeper mathematical concept with far-reaching implications. From the fundamental theorem of arithmetic to the sophisticated algorithms used in cryptography, the study of prime numbers and prime factorization continues to drive innovation and enhance security across numerous fields. Understanding the underlying principles and exploring the various methods for finding prime factorizations not only solidifies mathematical knowledge but also offers a glimpse into the intricate beauty and practical power of number theory. Whether you're a student learning the basics or a seasoned mathematician delving into complex algorithms, the journey of exploring prime factorization is a rewarding and enriching experience.
Latest Posts
Latest Posts
-
According To The Fluid Mosaic Model Of The Cell Membrane
Apr 02, 2025
-
What Is The Only Movable Bone Of The Skull
Apr 02, 2025
-
How Many Inches Are In One Meter
Apr 02, 2025
-
What Is The Freezing Point Of Water In Kelvin Scale
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Find The Prime Factorization Of 63 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
