What Is 4/9 As A Percent
Juapaving
Mar 26, 2025 · 4 min read
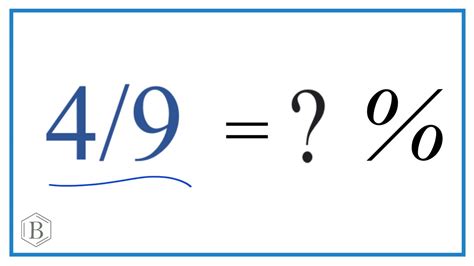
Table of Contents
- What Is 4/9 As A Percent
- Table of Contents
- What is 4/9 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversions
- Understanding Fractions and Percentages
- Converting 4/9 to a Percentage: The Step-by-Step Method
- Understanding Recurring Decimals and Rounding
- Practical Applications of Fraction-to-Percentage Conversions
- Advanced Concepts: Percentage Increase and Decrease
- Conclusion: Mastering Fraction-to-Percentage Conversions
- Latest Posts
- Latest Posts
- Related Post
What is 4/9 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in various fields. Understanding this process is crucial for anyone dealing with data analysis, financial calculations, or simply everyday problem-solving. This comprehensive guide will delve into the specifics of converting 4/9 to a percentage, providing a step-by-step explanation and exploring related concepts to solidify your understanding.
Understanding Fractions and Percentages
Before we dive into the conversion, let's clarify the core concepts:
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates how many parts make up the whole. For example, in the fraction 4/9, 4 is the numerator and 9 is the denominator.
Percentages: A percentage represents a fraction of 100. The symbol "%" signifies "per hundred." Essentially, a percentage expresses a proportion out of a total of 100. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Converting 4/9 to a Percentage: The Step-by-Step Method
There are two primary methods to convert 4/9 to a percentage:
Method 1: Using Division
-
Divide the numerator by the denominator: This step translates the fraction into its decimal equivalent. In this case, we divide 4 by 9: 4 ÷ 9 = 0.444... (the 4 repeats infinitely).
-
Multiply the decimal by 100: To express the decimal as a percentage, multiply it by 100. This shifts the decimal point two places to the right. 0.444... × 100 = 44.444...%
-
Round to the desired precision: Since the decimal portion repeats infinitely, we need to round the percentage to a specific number of decimal places. Commonly, we round to two decimal places: 44.44%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
While the division method is generally more straightforward, understanding this approach provides valuable insight into the relationship between fractions and percentages.
-
Find an equivalent fraction with a denominator of 100: To achieve this, we need to find a number that, when multiplied by 9, equals 100. Unfortunately, there isn't a whole number that satisfies this condition. Instead, we can use a proportion:
4/9 = x/100
-
Cross-multiply and solve for x: Cross-multiplying gives us:
9x = 400
-
Solve for x: Divide both sides by 9:
x = 400/9 ≈ 44.44
-
Express as a percentage: Since x represents the numerator when the denominator is 100, x is the percentage. Therefore, 4/9 is approximately 44.44%.
Understanding Recurring Decimals and Rounding
The conversion of 4/9 resulted in a recurring decimal (0.444...). Recurring decimals are decimals where one or more digits repeat infinitely. When expressing this as a percentage, it's crucial to understand the implications of rounding.
Rounding introduces a small degree of error. The more decimal places you use, the smaller the error, but you'll still have a slight deviation from the exact value. For most practical purposes, rounding to two decimal places (44.44%) provides sufficient accuracy. However, in certain applications requiring higher precision, more decimal places may be necessary.
Practical Applications of Fraction-to-Percentage Conversions
The ability to convert fractions to percentages has broad applications across various fields:
-
Finance: Calculating interest rates, discounts, profit margins, and tax rates often involves converting fractions to percentages.
-
Data Analysis: Representing data proportions using percentages makes it easier to understand and compare different data sets.
-
Science: Many scientific measurements and calculations involve expressing proportions as percentages.
-
Everyday Life: Calculating tips, understanding sale discounts, and interpreting statistics frequently utilize percentage calculations.
Advanced Concepts: Percentage Increase and Decrease
Building on the foundation of fraction-to-percentage conversions, we can explore more complex scenarios, such as percentage increase and decrease.
Percentage Increase: This involves calculating the percentage change when a value increases. The formula is:
Percentage Increase = [(New Value - Original Value) / Original Value] × 100%
Percentage Decrease: This calculates the percentage change when a value decreases. The formula is:
Percentage Decrease = [(Original Value - New Value) / Original Value] × 100%
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental skill with countless applications. Understanding both the division method and the equivalent fraction method provides a robust understanding of this concept. Remember to consider the implications of rounding recurring decimals and choose an appropriate level of precision based on the context. By mastering this skill, you'll be better equipped to tackle a wide range of mathematical problems and enhance your analytical abilities in various fields. Whether you're dealing with financial calculations, analyzing data, or solving everyday problems, this knowledge will be invaluable. Practice makes perfect, so continue practicing converting fractions to percentages to build proficiency and confidence in your mathematical abilities. Remember to always double-check your work to ensure accuracy. With consistent practice and a solid understanding of the underlying principles, you'll become proficient in performing these essential calculations with ease.
Latest Posts
Latest Posts
-
3 8 Expressed As A Percentage Is
Mar 27, 2025
-
Can The Orthocenter Be Outside The Triangle
Mar 27, 2025
-
Three Letter Words Beginning With X
Mar 27, 2025
-
What Is The Monomer Of A Dna Molecule
Mar 27, 2025
-
What Are All The Factors Of 23
Mar 27, 2025
Related Post
Thank you for visiting our website which covers about What Is 4/9 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
