What Is 30 As A Decimal
Juapaving
Mar 31, 2025 · 5 min read
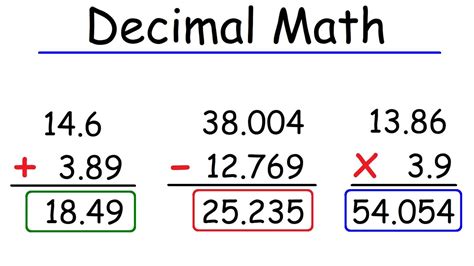
Table of Contents
What is 30 as a Decimal? A Comprehensive Exploration
The question, "What is 30 as a decimal?" might seem trivial at first glance. After all, 30 is already expressed as a whole number. However, understanding the underlying concepts of decimal representation, different number systems, and the relationship between whole numbers and decimals provides a valuable insight into the foundations of mathematics. This article will delve deeply into this seemingly simple question, exploring various perspectives and expanding upon the fundamental principles involved.
Understanding Decimal Representation
The decimal system, also known as the base-10 system, is the most commonly used number system globally. It's based on ten digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Each digit in a decimal number represents a power of 10. For instance, the number 30 can be broken down as follows:
- 3 x 10<sup>1</sup> (3 tens) + 0 x 10<sup>0</sup> (0 ones)
This representation clearly shows that 30 is a whole number, meaning it doesn't contain any fractional parts. The decimal point, crucial for representing numbers with fractional parts, is implicitly present after the 0, though we often omit it for whole numbers.
30 as a Decimal: Different Perspectives
While 30 is inherently a whole number, we can express it in various ways to highlight different aspects of decimal representation:
-
30.0: This explicitly shows the absence of any fractional part. The ".0" emphasizes that there are no tenths, hundredths, thousandths, or any other decimal places. This is particularly useful when comparing or working with numbers that do have decimal components.
-
30.000...: Extending the zeros infinitely further reinforces the concept of no fractional component. This representation is helpful when dealing with precision requirements in scientific or engineering contexts where even an infinitesimally small fractional error might be significant.
-
3 x 10<sup>1</sup>: This scientific notation highlights the magnitude of the number, emphasizing its place value within the decimal system. It's a more compact way to represent larger numbers and is particularly useful in fields like physics and computer science.
Comparing 30 to Other Decimal Numbers
Understanding 30 as a decimal becomes more meaningful when contrasted with numbers that do have fractional parts:
-
30.5: This number represents 30 and a half. The ".5" indicates 5 tenths (5/10). The difference between 30 and 30.5 highlights the role of the decimal point in distinguishing whole numbers from numbers with fractional components.
-
30.125: This number represents 30 and 125 thousandths (125/1000). The difference between 30, 30.5, and 30.125 demonstrates how decimal places increase precision.
-
29.999...: This recurring decimal approaches 30, but technically never reaches it. Understanding this subtle difference demonstrates a deeper understanding of limits and the nature of infinite series. It is crucial in calculus and other advanced mathematical disciplines.
Decimal Representation in Different Number Systems
While the decimal system is ubiquitous, other number systems exist. Understanding how 30 is represented in other bases helps clarify the fundamental principles of positional notation:
-
Binary (base-2): 30 in binary is 11110. Each digit represents a power of 2 (16 + 8 + 4 + 2 + 0 = 30).
-
Hexadecimal (base-16): 30 in hexadecimal is 1E. Hexadecimal utilizes digits 0-9 and the letters A-F to represent values 10-15.
-
Octal (base-8): 30 in octal is 36. Octal uses digits 0-7.
The differences in these representations emphasize that the decimal representation (30) is specific to the base-10 system. The underlying value remains the same, but its expression changes depending on the base used.
The Significance of Zero in Decimal Representation
The zero in 30 plays a crucial role:
-
Place Value: It indicates that there are no units (10<sup>0</sup>). Without the zero, the number would be interpreted as 3, not 30.
-
Magnitude: The zero significantly influences the magnitude of the number. Removing it alters the value by an order of magnitude (from 30 to 3).
-
Arithmetic Operations: The zero plays a vital role in arithmetic operations. Adding, subtracting, multiplying, or dividing 30 involves the zero directly in the calculation.
Applications of Understanding 30 as a Decimal
While the simple representation of 30 might seem basic, understanding its decimal representation has numerous practical applications across various fields:
-
Finance: Calculations involving monetary amounts frequently utilize decimal representation. Understanding decimal places is crucial for accurately calculating interest, taxes, and other financial transactions.
-
Engineering: In engineering, precise measurements and calculations are paramount. Decimal representation ensures accuracy in designing structures, circuits, and other engineering applications.
-
Computer Science: While computers use binary representation, understanding decimal equivalents is crucial for interacting with and interpreting computer outputs. Converting between decimal and binary representations is a fundamental skill in computer science.
-
Scientific Research: Data analysis in scientific research often involves large quantities of numerical data. Decimal representation allows for precise recording and analysis of experimental results.
-
Everyday Life: We encounter decimal numbers in numerous everyday situations, from measuring distances and weights to calculating prices and quantities.
Conclusion: Beyond the Obvious
The seemingly simple question of "What is 30 as a decimal?" opens up a rich exploration into the fundamental principles of number systems, decimal representation, and the importance of place value. Understanding these concepts lays the foundation for more advanced mathematical and scientific studies. By exploring different perspectives and contrasting 30 with other decimal numbers, we develop a deeper appreciation for the versatility and precision afforded by the decimal system. The seemingly simple number 30 becomes a gateway to a deeper understanding of the mathematical world around us. This detailed exploration aims not just to answer the question but to foster a stronger grasp of the underlying mathematical principles.
Latest Posts
Latest Posts
-
What Shape Has 12 Edges 8 Vertices And 6 Faces
Apr 02, 2025
-
Different Ways To Write A Number
Apr 02, 2025
-
Least Common Multiple Of 8 And 4
Apr 02, 2025
-
How Many Neutrons Are In Potassium
Apr 02, 2025
-
Relation Between Linear And Angular Acceleration
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
