What Is 3 7 As A Percent
Juapaving
Mar 21, 2025 · 5 min read
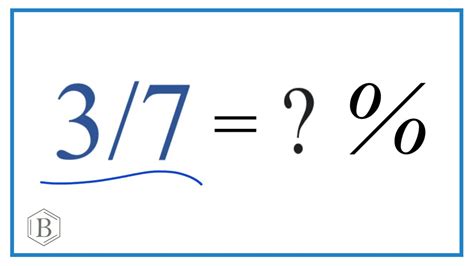
Table of Contents
What is 3/7 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversion
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in various fields, from finance and statistics to everyday calculations. This comprehensive guide will delve into the process of converting the fraction 3/7 into a percentage, explaining the method step-by-step, providing practical examples, and exploring related concepts. We'll also touch upon the significance of understanding fraction-to-percentage conversions and their use in real-world scenarios.
Understanding Fractions and Percentages
Before diving into the conversion, let's clarify the concepts of fractions and percentages.
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into. In our case, 3/7 means we have 3 parts out of a total of 7 equal parts.
Percentages: A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent" or "out of 100". For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100, or 1/2.
Converting 3/7 to a Percentage: The Step-by-Step Process
Converting a fraction to a percentage involves two main steps:
Step 1: Convert the fraction to a decimal. To do this, we divide the numerator (3) by the denominator (7):
3 ÷ 7 ≈ 0.42857
The result is an approximate decimal because the division results in a repeating decimal (0.42857142857...). We often round the decimal to a certain number of decimal places for practicality. For this example, we'll use five decimal places.
Step 2: Convert the decimal to a percentage. To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol:
0.42857 × 100 ≈ 42.857%
Therefore, 3/7 is approximately equal to 42.857%.
Rounding and Precision
The precision of the percentage depends on the context. In some cases, a rounded percentage is sufficient, while in others, greater accuracy is required.
- Rounding to the nearest whole number: 43%
- Rounding to one decimal place: 42.9%
- Rounding to two decimal places: 42.86%
The level of rounding should be chosen based on the required level of accuracy for the specific application. For most everyday purposes, rounding to one or two decimal places is adequate. However, in scientific or financial contexts, higher precision may be necessary.
Alternative Methods for Conversion
While the method described above is the most straightforward, there are other ways to approach the conversion of 3/7 to a percentage.
Method 2: Using Proportions
We can set up a proportion to solve for the percentage:
3/7 = x/100
Cross-multiplying, we get:
7x = 300
Solving for x:
x = 300/7 ≈ 42.857
Therefore, x ≈ 42.857%, confirming our previous result.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies the conversion. Simply enter the fraction as 3 ÷ 7 and then multiply by 100 to obtain the percentage.
Practical Applications of Fraction-to-Percentage Conversion
The ability to convert fractions to percentages is crucial in various real-world scenarios:
-
Finance: Calculating interest rates, discounts, profit margins, and tax rates often involves working with percentages. Understanding how fractions relate to percentages is vital for accurate financial calculations.
-
Statistics: Many statistical analyses involve expressing data as percentages. For instance, representing survey results, calculating probabilities, and interpreting data often requires converting fractions to percentages for clearer understanding.
-
Everyday Life: Calculating tips, discounts at stores, or understanding the nutritional content of food often requires converting fractions to percentages.
-
Science: Scientific data is often expressed as percentages to represent proportions or ratios.
-
Education: Understanding fraction-to-percentage conversion is crucial for solving various problems across different academic subjects, such as mathematics, science, and economics.
Understanding Repeating Decimals in Percentage Conversions
As you noticed earlier, the decimal representation of 3/7 is a repeating decimal (0.42857142857...). This means the digits repeat infinitely. When converting such decimals to percentages, we must decide on an appropriate level of rounding to obtain a practical and usable value. Ignoring the repeating nature entirely would lead to inaccuracies in calculations.
Beyond 3/7: Generalizing the Conversion Process
The method we used to convert 3/7 to a percentage can be applied to any fraction:
- Divide the numerator by the denominator to obtain a decimal.
- Multiply the decimal by 100 to obtain the percentage.
- Round the percentage to the desired level of precision.
This process provides a reliable and efficient way to convert any fraction to its percentage equivalent.
Conclusion: Mastering Fraction-to-Percentage Conversions
Mastering the conversion of fractions to percentages is essential for numerous applications in various aspects of life. Understanding the underlying principles and applying the correct method ensures accurate and efficient calculations. The examples and explanations provided in this guide should equip you with the necessary tools to confidently convert any fraction into its percentage equivalent, enabling you to tackle a wider range of problems and applications requiring this fundamental mathematical skill. Remember to always consider the appropriate level of rounding based on the context and desired accuracy. This guide has focused on the specific example of 3/7, but the techniques presented are broadly applicable across all fraction-to-percentage conversions. By understanding these principles and practicing regularly, you will enhance your mathematical proficiency and confidently navigate situations requiring this crucial skill.
Latest Posts
Latest Posts
-
Why Are Leaves Green In Colour
Mar 28, 2025
-
What Type Of Mixture Is Concrete
Mar 28, 2025
-
Five Letter Word Ending In E R
Mar 28, 2025
-
The Largest Endocrine Gland Is The
Mar 28, 2025
-
What Can 51 Be Divided By
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 7 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
