What Are The Factors Of 89
Juapaving
Mar 26, 2025 · 5 min read
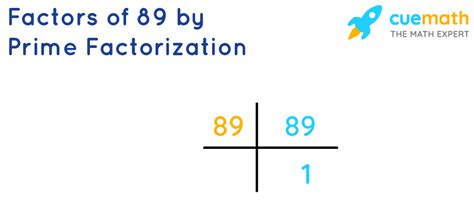
Table of Contents
What are the Factors of 89? A Deep Dive into Prime Numbers and Factorization
The seemingly simple question, "What are the factors of 89?" opens a door to a fascinating world of number theory, prime numbers, and the fundamental building blocks of mathematics. While the answer itself is straightforward, exploring the concept behind it reveals a richer understanding of numerical relationships and the methods used to determine factors. This article will not only answer the question directly but will delve into the broader context of prime factorization, its applications, and its significance in mathematics.
Understanding Factors and Divisibility
Before tackling the factors of 89, let's define some key terms. A factor (or divisor) of a number is a whole number that divides that number exactly without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 without leaving a remainder. Divisibility rules provide shortcuts to determine if a number is a factor of another. For instance, a number is divisible by 2 if it's even, by 3 if the sum of its digits is divisible by 3, and by 5 if it ends in 0 or 5.
Identifying the Factors of 89
Now, let's address the core question: what are the factors of 89? The process of finding factors involves systematically checking each whole number to see if it divides 89 without a remainder. We can start by checking the smallest whole numbers:
- 1: 89 divided by 1 is 89, so 1 is a factor.
- 2: 89 is not divisible by 2 because it's an odd number.
- 3: The sum of the digits of 89 (8 + 9 = 17) is not divisible by 3, so 89 is not divisible by 3.
- 4: 89 is not divisible by 4 because it's not divisible by 2.
- 5: 89 does not end in 0 or 5, so it's not divisible by 5.
- 7: 89 divided by 7 is approximately 12.7, so 7 is not a factor.
- ...and so on.
Continuing this process, we'll find that the only whole numbers that divide 89 without a remainder are 1 and 89 itself. Therefore, the factors of 89 are 1 and 89.
89: A Prime Number
The fact that 89 only has two factors, 1 and itself, categorizes it as a prime number. Prime numbers are fundamental in number theory because they are the building blocks of all other whole numbers. Every composite number (a whole number greater than 1 that is not prime) can be expressed as a unique product of prime numbers. This is known as the Fundamental Theorem of Arithmetic.
Properties of Prime Numbers
Prime numbers possess several unique properties:
- Only two factors: As mentioned, prime numbers only have two positive divisors: 1 and the number itself.
- Infinite in quantity: There are infinitely many prime numbers; this fact has been proven mathematically.
- Distribution: While prime numbers appear randomly, there are patterns and conjectures about their distribution along the number line. The Prime Number Theorem provides an approximation of the number of primes less than a given number.
- Importance in Cryptography: Prime numbers play a crucial role in modern cryptography, forming the basis of many encryption algorithms that secure online communications and transactions.
Prime Factorization and its Applications
The process of expressing a composite number as a product of its prime factors is called prime factorization. For example, the prime factorization of 12 is 2 x 2 x 3 (or 2² x 3). Prime factorization has numerous applications in various fields:
- Mathematics: It's fundamental to simplifying fractions, finding the least common multiple (LCM) and greatest common divisor (GCD) of numbers, and solving various mathematical problems.
- Computer Science: Prime factorization is essential in cryptography, as mentioned earlier. It's also used in algorithms for data compression and other computational tasks.
- Cryptography: The difficulty of factoring large numbers into their prime factors is the basis of many modern encryption systems, ensuring the security of sensitive data.
- Coding Theory: Prime numbers play a role in error correction codes, which are used to detect and correct errors in data transmission.
Methods for Finding Prime Factors
Several methods can be used to find the prime factors of a number:
- Trial division: This involves systematically dividing the number by prime numbers, starting with the smallest prime (2), and continuing until all prime factors are found. This method is simple but can be time-consuming for large numbers.
- Factor trees: This is a visual method that breaks down a number into smaller factors until all factors are prime.
- Sieve of Eratosthenes: This is a powerful algorithm for finding all prime numbers up to a specified limit. It's efficient for identifying many primes simultaneously.
- Advanced Algorithms: For very large numbers, more sophisticated algorithms such as the general number field sieve are employed. These algorithms are computationally intensive and require powerful computers.
The Significance of 89's Primeness
The fact that 89 is a prime number highlights the fundamental nature of prime numbers in the structure of integers. Its primeness means it cannot be further broken down into smaller whole number factors, underscoring its role as a basic building block in number theory. While seemingly a simple number, 89 represents an instance of the infinite sequence of prime numbers, each with its unique mathematical properties and significance. Understanding prime numbers, exemplified by analyzing the factors of 89, provides a deeper appreciation for the fundamental concepts of mathematics and their wider implications.
Conclusion
The factors of 89 are simply 1 and 89. However, the journey to this answer reveals a deeper understanding of prime numbers, prime factorization, and their significance across multiple fields. From cryptography to fundamental mathematical theorems, prime numbers like 89 form the foundation of many crucial concepts. This exploration underscores the importance of understanding the basic building blocks of numbers and the powerful implications of their unique properties. The seemingly simple question regarding the factors of 89 opens doors to a complex and fascinating world of mathematical exploration.
Latest Posts
Latest Posts
-
Solve X 3 1 7 15
Mar 29, 2025
-
How Much Cerebral Capacity Do Dolphins Use
Mar 29, 2025
-
The Original Three Components Of The Cell Theory Are That
Mar 29, 2025
-
Give The Temperature And Pressure At Stp
Mar 29, 2025
-
Give The Ground State Electron Configuration For Pb
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Are The Factors Of 89 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
