What Are Common Multiples Of 6 And 8
Juapaving
Mar 28, 2025 · 5 min read
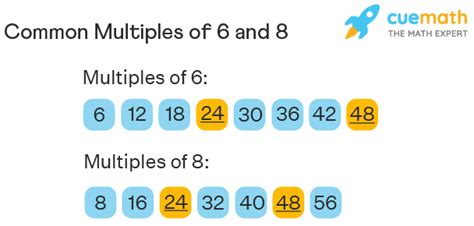
Table of Contents
What Are the Common Multiples of 6 and 8? A Deep Dive into Number Theory
Finding common multiples, especially for seemingly simple numbers like 6 and 8, might seem straightforward at first glance. However, understanding the underlying concepts reveals a fascinating area of number theory with practical applications beyond basic arithmetic. This article will explore the common multiples of 6 and 8, delve into the methods for finding them, and discuss their significance in various mathematical contexts.
Understanding Multiples and Common Multiples
Before diving into the specifics of 6 and 8, let's establish a foundational understanding of multiples and common multiples.
What is a Multiple?
A multiple of a number is the product of that number and any integer (whole number). For example:
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, and so on.
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, and so on.
Notice that the multiples extend infinitely in both positive and negative directions. However, we usually focus on the positive multiples.
What are Common Multiples?
Common multiples are numbers that are multiples of two or more numbers. Looking at the multiples of 6 and 8 above, we can see some numbers appear in both lists: 24, 48... These are common multiples of 6 and 8.
Finding Common Multiples of 6 and 8: Methods and Techniques
There are several ways to identify the common multiples of 6 and 8. Let's explore the most common approaches:
1. Listing Multiples: A Simple Approach (Suitable for Smaller Numbers)
The simplest method, especially for smaller numbers like 6 and 8, is to list out the multiples of each number and identify the common ones. While effective for small numbers, this method becomes cumbersome for larger numbers.
Multiples of 6: 6, 12, 18, 24, 30, 36, 48, 54, 60, 72, 78, 84, 90, 96, 102, 108, 114, 120... Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120...
Common Multiples: 24, 48, 72, 96, 120...
2. Prime Factorization: A More Efficient Method
Prime factorization provides a more efficient method, especially when dealing with larger numbers. It involves breaking down each number into its prime factors.
- Prime factorization of 6: 2 x 3
- Prime factorization of 8: 2 x 2 x 2 = 2³
To find the least common multiple (LCM), we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3¹ = 3
LCM(6, 8) = 8 x 3 = 24
Once you have the LCM, you can find other common multiples by multiplying the LCM by integers:
- 24 x 1 = 24
- 24 x 2 = 48
- 24 x 3 = 72
- 24 x 4 = 96
- 24 x 5 = 120
- and so on...
This method is significantly more efficient than listing multiples, especially when dealing with larger numbers or multiple numbers.
3. Using the Formula: LCM and GCD
The least common multiple (LCM) is intrinsically linked to the greatest common divisor (GCD). The relationship is expressed in the formula:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the numbers.
To use this method, we first find the GCD of 6 and 8. The GCD is the largest number that divides both 6 and 8 without leaving a remainder. In this case, GCD(6, 8) = 2.
Now, using the formula:
LCM(6, 8) x 2 = 6 x 8 LCM(6, 8) x 2 = 48 LCM(6, 8) = 48 / 2 = 24
Again, we find the LCM to be 24, and other common multiples are multiples of 24. This method is particularly useful when working with larger numbers where finding the GCD is relatively easier than directly calculating the LCM.
Least Common Multiple (LCM) and its Significance
The least common multiple (LCM) is the smallest positive number that is a multiple of both numbers. In our case, the LCM of 6 and 8 is 24. The LCM is crucial in various mathematical applications:
- Fraction Addition and Subtraction: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is essential to find a common denominator.
- Scheduling and Cyclical Events: The LCM is used to determine when events with different cycles will occur simultaneously. For instance, if one event repeats every 6 days and another every 8 days, the LCM (24) determines when they will coincide.
- Modular Arithmetic: The LCM plays a vital role in solving problems in modular arithmetic, a branch of number theory with applications in cryptography and computer science.
Beyond the Basics: Exploring Further Concepts
The concept of common multiples extends beyond simply finding the numbers. Let's explore some further concepts:
Infinite Number of Common Multiples
It's crucial to understand that there are an infinite number of common multiples for any two numbers (unless one is zero). While we often focus on the LCM, the set of common multiples is unbounded.
Common Multiples and Sets
We can represent the common multiples of 6 and 8 as a set: {24, 48, 72, 96, 120, ...}. This set is an infinite set. Set theory provides a formal way to represent and manipulate these collections of numbers.
Application in Real-World Scenarios
The concept of common multiples has practical applications in various real-world scenarios:
- Construction: Determining the optimal lengths for materials to avoid wastage.
- Manufacturing: Coordinating production cycles for different components.
- Music: Understanding harmonic intervals and musical scales (which often rely on relationships between multiples).
Conclusion: Mastering Common Multiples
Understanding common multiples, particularly the methods for finding them, is fundamental to various mathematical concepts and practical applications. From the simple listing of multiples to the more efficient prime factorization and GCD/LCM methods, choosing the appropriate technique depends on the context and the numbers involved. Mastering these methods equips you with a powerful tool for solving problems in number theory and beyond. Remember, the seemingly simple concept of common multiples unlocks a rich landscape of mathematical possibilities and real-world applications. The infinite nature of common multiples highlights the depth and complexity inherent in even seemingly basic arithmetic concepts. Therefore, a thorough grasp of this topic lays a strong foundation for further exploration in mathematics and its applications.
Latest Posts
Latest Posts
-
What Is The Percentage Of 2 5
Mar 31, 2025
-
How To Find Reciprocal Of A Mixed Number
Mar 31, 2025
-
Which Of The Following Is Considered A Micronutrient
Mar 31, 2025
-
How Many Inches Is 2 Meters
Mar 31, 2025
-
What Medical Problem Afflicts Mrs Mallard
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Are Common Multiples Of 6 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
