What Are All The Factors Of 80
Juapaving
Mar 28, 2025 · 6 min read
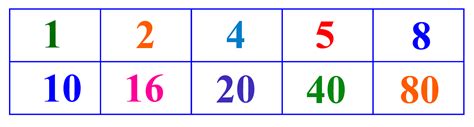
Table of Contents
What are all the factors of 80? A Comprehensive Exploration
Finding all the factors of a number might seem like a simple mathematical task, but understanding the process and its implications opens doors to more complex concepts in number theory. This article delves deep into finding all the factors of 80, explaining the methodology in a clear and accessible way, and exploring related mathematical ideas. We'll go beyond simply listing the factors, examining the concepts of prime factorization, divisibility rules, and even touching upon the significance of factors in different mathematical fields.
Understanding Factors
Before we dive into the specifics of 80, let's establish a firm understanding of what constitutes a factor. A factor (or divisor) of a number is a whole number that divides the original number evenly, leaving no remainder. In other words, if 'a' is a factor of 'b', then b/a results in a whole number.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because each of these numbers divides 12 without leaving a remainder.
Finding the Factors of 80: A Step-by-Step Approach
Several methods can be used to determine the factors of 80. Let's explore the most common and effective approaches:
1. Systematic Listing:
The simplest method involves systematically checking each number from 1 up to 80 to see if it divides 80 evenly. While straightforward, this can be time-consuming for larger numbers.
Let's start:
- 1: 80/1 = 80 (1 is always a factor)
- 2: 80/2 = 40
- 4: 80/4 = 20
- 5: 80/5 = 16
- 8: 80/8 = 10
- 10: 80/10 = 8
- 16: 80/16 = 5
- 20: 80/20 = 4
- 40: 80/40 = 2
- 80: 80/80 = 1 (The number itself is always a factor)
Therefore, the factors of 80 are 1, 2, 4, 5, 8, 10, 16, 20, 40, and 80.
2. Prime Factorization:
This method is more efficient, especially for larger numbers. It involves breaking down the number into its prime factors. Prime numbers are whole numbers greater than 1 that have only two divisors: 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
The prime factorization of 80 is: 2 x 2 x 2 x 2 x 5 = 2<sup>4</sup> x 5
Once you have the prime factorization, you can systematically find all the factors. This involves creating combinations of the prime factors.
- Using only 2: 2<sup>1</sup> = 2, 2<sup>2</sup> = 4, 2<sup>3</sup> = 8, 2<sup>4</sup> = 16
- Using only 5: 5<sup>1</sup> = 5
- Combining 2 and 5: 2 x 5 = 10, 2<sup>2</sup> x 5 = 20, 2<sup>3</sup> x 5 = 40, 2<sup>4</sup> x 5 = 80
And of course, 1 is always a factor. This method neatly provides all the factors: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80.
3. Pairwise Approach:
This method leverages the fact that factors often come in pairs. Once you find one factor, you automatically know its corresponding pair. For instance, if 2 is a factor, then 80/2 = 40 is also a factor.
Start by listing the smaller factors and find their corresponding pairs:
- 1 and 80
- 2 and 40
- 4 and 20
- 5 and 16
- 8 and 10
This method efficiently identifies all factor pairs.
Beyond the Factors: Exploring Related Concepts
The process of finding factors opens doors to several key mathematical concepts:
1. Divisibility Rules:
Understanding divisibility rules can significantly speed up the process of identifying factors. For example:
- Divisibility by 2: A number is divisible by 2 if its last digit is even (0, 2, 4, 6, 8). 80 is divisible by 2.
- Divisibility by 5: A number is divisible by 5 if its last digit is 0 or 5. 80 is divisible by 5.
- Divisibility by 10: A number is divisible by 10 if its last digit is 0. 80 is divisible by 10.
Knowing these rules helps you quickly eliminate numbers that are not factors.
2. Greatest Common Factor (GCF):
The Greatest Common Factor (GCF), also known as the Highest Common Factor (HCF), is the largest number that divides two or more numbers without leaving a remainder. Finding the GCF is crucial in simplifying fractions and solving various algebraic problems.
For example, if we want to find the GCF of 80 and 100, we can list their factors and find the largest common one. The factors of 80 are 1, 2, 4, 5, 8, 10, 16, 20, 40, 80. The factors of 100 are 1, 2, 4, 5, 10, 20, 25, 50, 100. The GCF of 80 and 100 is 20.
3. Least Common Multiple (LCM):
The Least Common Multiple (LCM) is the smallest number that is a multiple of two or more numbers. Finding the LCM is essential in solving problems involving fractions and in areas like scheduling and cyclical events.
To find the LCM of 80 and 100, one method is to list their multiples until you find the smallest common one. A more efficient method uses the prime factorization.
The prime factorization of 80 is 2<sup>4</sup> x 5. The prime factorization of 100 is 2<sup>2</sup> x 5<sup>2</sup>.
The LCM is found by taking the highest power of each prime factor present in either number: 2<sup>4</sup> x 5<sup>2</sup> = 400.
4. Number Theory Applications:
Understanding factors has broad applications in number theory. Concepts like perfect numbers (numbers equal to the sum of their proper divisors), abundant numbers (numbers where the sum of their proper divisors is greater than the number itself), and deficient numbers (numbers where the sum of their proper divisors is less than the number itself) all rely on the analysis of factors.
80 is an example of an abundant number because the sum of its proper divisors (1 + 2 + 4 + 5 + 8 + 10 + 16 + 20 + 40 = 106) is greater than 80 itself.
Conclusion: The Significance of Factors
This comprehensive exploration of the factors of 80 demonstrates that even a seemingly simple mathematical problem can lead to a deeper understanding of fundamental concepts in number theory. The methods presented – systematic listing, prime factorization, and the pairwise approach – offer different strategies for finding factors, each with its own strengths and weaknesses. Moreover, the discussion extended beyond simply listing the factors to highlight the importance of factors in determining the greatest common factor, the least common multiple, and the broader application in number theory. Understanding factors is not just about finding divisors; it's about unlocking a deeper appreciation for the intricate relationships between numbers.
Latest Posts
Latest Posts
-
Plants Exchange Gas With The Atmosphere
Mar 31, 2025
-
Numbers In Words 1 To 1000000
Mar 31, 2025
-
Digestion Of Food Is A Physical Or Chemical Change
Mar 31, 2025
-
What Is The Prime Factorization For 63
Mar 31, 2025
-
What Soil Type Holds The Most Water
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Are All The Factors Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
