What Are 3 Fractions Equivalent To 3/8
Juapaving
Mar 21, 2025 · 5 min read
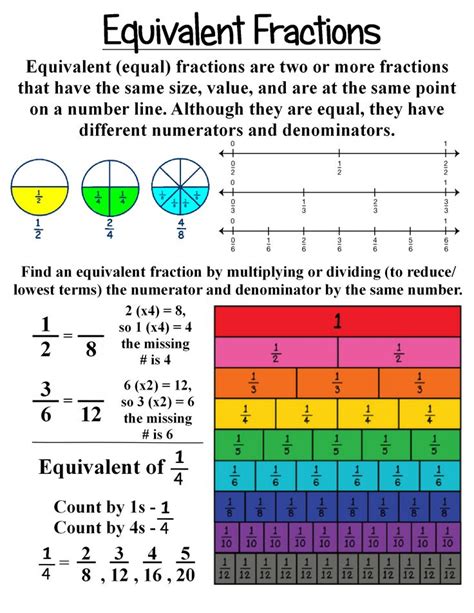
Table of Contents
What Are 3 Fractions Equivalent to 3/8? A Deep Dive into Equivalent Fractions
Finding equivalent fractions might seem like a simple task, especially when dealing with a fraction like 3/8. However, understanding the underlying principles and exploring various methods can significantly enhance your grasp of this fundamental concept in mathematics. This comprehensive guide delves into the intricacies of equivalent fractions, focusing specifically on finding three fractions equivalent to 3/8, while also expanding on the broader topic to provide a solid foundation for anyone working with fractions.
Understanding Equivalent Fractions: The Core Concept
Equivalent fractions represent the same proportion or value despite having different numerators and denominators. Imagine slicing a pizza: a pizza cut into 8 slices with 3 taken represents the same amount as a pizza cut into 16 slices with 6 taken, or even a pizza cut into 24 slices with 9 taken. These all represent the same portion – 3/8. The key is that the ratio between the numerator and the denominator remains constant.
To find equivalent fractions, you need to multiply or divide both the numerator and the denominator by the same non-zero number. This ensures that the ratio remains unchanged, maintaining the fractional value. Multiplying essentially increases the number of slices (denominator) and the number of slices taken (numerator) proportionally, while dividing does the opposite, reducing the number of slices while maintaining the proportion.
Finding Three Fractions Equivalent to 3/8: The Methods
Let's explore three methods to discover three fractions equivalent to 3/8:
Method 1: Multiplying by a Whole Number
The simplest method involves multiplying both the numerator and the denominator by the same whole number. Let's choose three different whole numbers: 2, 3, and 4.
- Multiplying by 2: (3 x 2) / (8 x 2) = 6/16
- Multiplying by 3: (3 x 3) / (8 x 3) = 9/24
- Multiplying by 4: (3 x 4) / (8 x 4) = 12/32
Therefore, three fractions equivalent to 3/8 are 6/16, 9/24, and 12/32. These fractions, while appearing different, all represent the same portion of a whole.
Method 2: Using a Common Factor
This method is particularly useful when you need to simplify fractions or find equivalent fractions with smaller numbers. We can start with a simplified fraction and then multiply to increase the numerator and denominator. Since 3/8 is already in its simplest form (3 and 8 share no common factors other than 1), we'll use multiplication to find our equivalents. Let's use factors such as 5, 7, and 11.
- Multiplying by 5: (3 x 5) / (8 x 5) = 15/40
- Multiplying by 7: (3 x 7) / (8 x 7) = 21/56
- Multiplying by 11: (3 x 11) / (8 x 11) = 33/88
This gives us another set of equivalent fractions: 15/40, 21/56, and 33/88.
Method 3: Visual Representation and Pattern Recognition
Visualizing fractions using diagrams can be incredibly helpful, especially for beginners. Imagine a rectangle divided into 8 equal parts, with 3 parts shaded to represent 3/8. To find equivalent fractions, you can simply divide the rectangle into more sections while keeping the same proportion shaded.
- Dividing into 16: If you divide each of the 8 parts into two, you now have 16 parts, and 6 of them would be shaded (6/16).
- Dividing into 24: Dividing each of the 8 parts into three would result in 24 parts, with 9 shaded (9/24).
- Dividing into 32: Dividing each of the 8 parts into four results in 32 parts, with 12 shaded (12/32).
This visual method reinforces the concept that dividing the whole into more parts and proportionally increasing the number of shaded parts maintains the overall proportion, creating equivalent fractions.
Beyond 3/8: Exploring the Broader Concept of Equivalent Fractions
The principles discussed above apply to any fraction. To find equivalent fractions for any given fraction, simply multiply or divide both the numerator and denominator by the same non-zero number. This process is essential for various mathematical operations, including:
- Adding and Subtracting Fractions: You often need to find equivalent fractions with a common denominator before performing these operations.
- Comparing Fractions: It’s easier to compare fractions with the same denominator. Finding equivalent fractions helps in this comparison.
- Simplifying Fractions: Dividing both the numerator and denominator by their greatest common divisor (GCD) simplifies a fraction to its lowest terms.
- Solving Equations: Equivalent fractions are frequently used in solving algebraic equations involving fractions.
Practical Applications and Real-World Examples
Equivalent fractions aren't just an abstract mathematical concept; they have numerous real-world applications. Consider these examples:
- Cooking and Baking: Recipes often require fractions of ingredients. Understanding equivalent fractions allows you to adapt recipes, for instance, doubling a recipe using equivalent fractions of ingredients. If a recipe calls for 1/4 cup of sugar, you can easily use 2/8 cup instead.
- Measurement and Construction: In construction and engineering, precise measurements are critical. Converting between different units (e.g., inches to feet) often involves working with equivalent fractions.
- Data Analysis and Statistics: Representing data using fractions and understanding equivalent fractions simplifies comparisons and interpretations.
- Finance and Budgeting: Understanding proportions and equivalent fractions aids in managing finances, calculating percentages, and understanding financial ratios.
Common Mistakes to Avoid When Working with Equivalent Fractions
While the concept seems straightforward, some common mistakes can arise:
- Only multiplying or dividing the numerator or denominator: Remember, both the numerator and the denominator must be multiplied or divided by the same number.
- Using zero as the multiplier or divisor: Dividing by zero is undefined in mathematics.
- Incorrectly simplifying fractions: Make sure to find the greatest common divisor (GCD) to simplify a fraction to its lowest terms.
Conclusion: Mastering the Art of Equivalent Fractions
Mastering the concept of equivalent fractions is fundamental for success in mathematics and its various applications. This detailed guide provided various methods to find three fractions equivalent to 3/8, reinforcing the understanding of the underlying principle of maintaining the same ratio between the numerator and the denominator. By understanding and applying these principles, you'll develop a stronger foundation in mathematics and enhance your problem-solving abilities across diverse fields. Remember to practice regularly and utilize the different approaches outlined here to build a comprehensive understanding of this critical mathematical concept. The more you practice, the easier it will become to identify and work with equivalent fractions confidently and accurately.
Latest Posts
Latest Posts
-
Sucrose And Lactose Are Examples Of
Mar 28, 2025
-
Which Of The Following Are True About Algae
Mar 28, 2025
-
Which Region Of The Nephron Is Impermeable To Water
Mar 28, 2025
-
What Is The Lcm Of 7 21
Mar 28, 2025
-
In The Periodic Table Horizontal Rows Are Called
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about What Are 3 Fractions Equivalent To 3/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
