What Angle To Join 3 Right Isosceles Triangles
Juapaving
Apr 02, 2025 · 5 min read
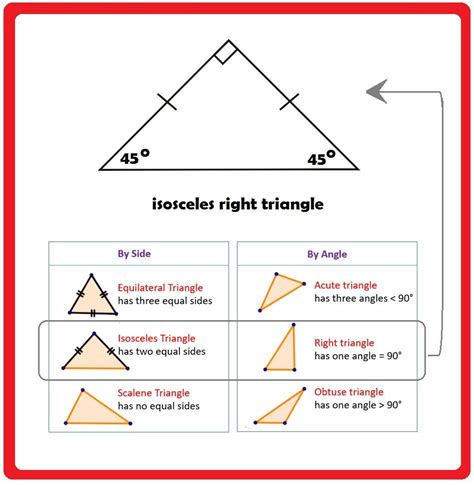
Table of Contents
What Angle to Join 3 Right Isosceles Triangles? Exploring Geometric Configurations
Joining three right isosceles triangles presents a fascinating geometric puzzle with multiple solutions, depending on the desired outcome. This article explores various approaches to combining these triangles, examining the angles involved, and highlighting the resulting shapes and their properties. We'll delve into different configurations, analyzing the angles needed to seamlessly connect the triangles and creating aesthetically pleasing and mathematically intriguing compositions. We'll also touch upon the practical applications and creative possibilities these configurations offer.
Understanding the Building Blocks: Right Isosceles Triangles
Before diving into the configurations, let's establish a clear understanding of our fundamental building blocks: right isosceles triangles. These triangles are characterized by:
- Two equal sides (legs): These sides are adjacent to the right angle.
- A right angle (90°): The angle formed by the two equal sides.
- Two equal acute angles (45°): The remaining angles are equal and measure 45° each, since the sum of angles in a triangle is always 180°.
This inherent symmetry and the 45° angles are key to understanding how these triangles can be joined to create various shapes.
Configuration 1: Forming a Larger Isosceles Triangle
The simplest configuration involves joining three right isosceles triangles to create a larger isosceles triangle. This is achieved by:
- Connecting the hypotenuses: Align the hypotenuses of two right isosceles triangles to form a straight line.
- Adding the third triangle: Place the third triangle such that its legs align with the legs of the other two triangles, forming the sides of a larger isosceles triangle.
Angles Involved: The angles involved in this configuration are primarily 45° and 90°, maintaining the isosceles nature of the resulting shape. The internal angles of the larger triangle are 90°, 45°, and 45°.
Configuration 2: Creating a Square
Another straightforward configuration uses three right isosceles triangles to create a square. This approach requires:
- Two triangles forming half a square: Two right isosceles triangles can be joined at their hypotenuses to form a square with a diagonal.
- The third triangle completing the square: The third triangle is then placed to fill the remaining triangular section, completing the square.
Angles Involved: This approach involves primarily 90° angles, which are inherent to the square's structure. However, the constituent triangles maintain their 45° angles.
Configuration 3: Constructing a Regular Hexagon (with additional steps)
While not directly achieved by merely joining the three triangles, constructing a regular hexagon involves utilizing right isosceles triangles as building blocks. This is achieved using the following steps, which will involve more than just three triangles:
- Creating equilateral triangles: Two right isosceles triangles can be joined to create an equilateral triangle with a side length equal to the hypotenuse of each individual right isosceles triangle.
- Building the hexagon: Six of these equilateral triangles can be arranged around a central point to create a regular hexagon. This approach would require six, not just three, right isosceles triangles.
Angles Involved: In the resulting hexagon, all internal angles measure 120°, with the original 45° angles of the triangles contributing to the formation of these 120° angles.
Configuration 4: Exploring Irregular Polygons
Beyond regular polygons, numerous irregular polygons can be created by joining three right isosceles triangles. The angles involved will depend heavily on the specific arrangement:
- Arbitrary joining: Joining triangles at various angles will produce polygons with a wide variety of internal angles. The resulting shapes can be irregular pentagons, hexagons, or more complex polygons.
- Controlling Angles: By strategically controlling the angles at which the triangles are connected, it's possible to create polygons with specific internal angle combinations. This requires careful consideration of trigonometric relationships.
Angles Involved: The angles involved in these configurations will vary greatly and are no longer restricted to 45° and 90°.
Configuration 5: 3D Structures
The versatility extends to three-dimensional structures. Imagine the triangles as facets of a larger shape:
- Pyramids: Three right isosceles triangles can form a three-sided pyramid (triangular pyramid or tetrahedron) but will not be a regular tetrahedron unless further triangles are added.
- More complex 3D shapes: By strategically connecting more right isosceles triangles, significantly more complex three-dimensional structures can be built.
Angles Involved: In three-dimensional structures, the angles involved become more complex and involve dihedral angles (angles between faces) in addition to the internal angles of the triangles.
Mathematical Considerations and Applications
Understanding the angle relationships inherent in these configurations is crucial for various applications:
- Tessellations: Investigating how these triangles can tessellate (tile a plane) without gaps or overlaps leads to explorations in geometry and pattern formation.
- Computer Graphics: In computer graphics and game development, understanding how to connect these triangles efficiently is vital for creating polygons, 3D models and textures.
- Architectural Design: Right isosceles triangles and their combinations find applications in architectural design where specific angles and symmetric shapes are desirable.
Creative Exploration and Artistic Expression
Beyond mathematical applications, exploring configurations of right isosceles triangles offers significant artistic and design potential:
- Mosaics: These triangles can form the basis for intricate mosaics.
- Patterns and Designs: The shapes derived by joining the triangles can be used to create stunning patterns and designs in various mediums.
- Jewelry Making: The symmetric nature lends itself well to jewelry creation.
Conclusion: A World of Possibilities
Joining three right isosceles triangles opens a world of geometric exploration and creative possibilities. While forming a larger isosceles triangle or square represents basic configurations, manipulating the arrangement allows for the construction of more complex shapes and structures. The angles involved, ranging from the straightforward 45° and 90° in simple configurations to more varied angles in complex arrangements, determine the final shape. By understanding these angle relationships and applying creative thinking, you can build upon the foundations of these simple triangles to create a fascinating variety of geometric designs and three-dimensional forms. The possibilities are limited only by your imagination and understanding of geometric principles. The more you explore these geometric puzzle-like arrangements, the deeper your understanding of shapes, angles, and their interaction will become. This exploration can serve as both a valuable mathematical exercise and a fertile ground for artistic and design innovation.
Latest Posts
Latest Posts
-
Find The Unit Vector In The Direction Of V
Apr 03, 2025
-
5 Letter Words Starting With Ho
Apr 03, 2025
-
Partial Fraction Decomposition Calculator Step By Step
Apr 03, 2025
-
5 Letter Words Starting With Har
Apr 03, 2025
-
Predict The Major Product For The Following Reaction
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Angle To Join 3 Right Isosceles Triangles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
