Triangle With Two Equal Sides Is Called
Juapaving
Mar 26, 2025 · 6 min read
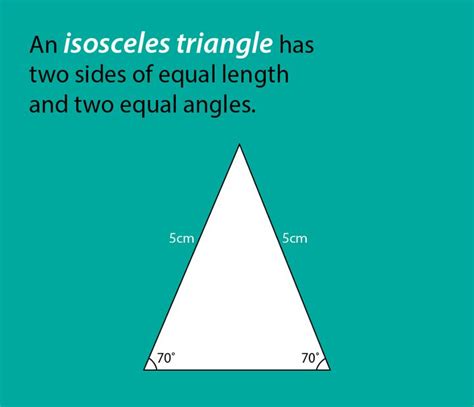
Table of Contents
A Triangle with Two Equal Sides is Called an Isosceles Triangle: A Deep Dive into Geometry
A triangle, the most fundamental polygon in geometry, is a closed two-dimensional figure formed by three line segments called sides. These sides meet at three points, forming the triangle's vertices or corners. Triangles are classified based on their side lengths and angles. One specific type, characterized by two sides of equal length, is known as an isosceles triangle. This article explores the properties, theorems, and applications of isosceles triangles in detail.
Defining an Isosceles Triangle
An isosceles triangle is defined as a triangle with at least two sides of equal length. These equal sides are called the legs of the triangle, while the third side is called the base. The angles opposite the equal sides are called the base angles, and the angle opposite the base is called the vertex angle or apex angle. It's crucial to remember the "at least" part of the definition. While many people think of an isosceles triangle as having exactly two equal sides, an equilateral triangle (with all three sides equal) is also considered a special case of an isosceles triangle.
Properties of Isosceles Triangles
Isosceles triangles possess several key properties that distinguish them from other types of triangles:
1. Base Angles are Equal:
This is arguably the most important property of an isosceles triangle. The base angles are always equal. This is a fundamental theorem in geometry and is frequently used in proofs and problem-solving. This property holds true regardless of the size or orientation of the triangle.
2. Altitude, Median, Angle Bisector, and Perpendicular Bisector of the Base are Concurrency:
In an isosceles triangle, the altitude (the perpendicular line from the vertex angle to the base), the median (the line segment from the vertex angle to the midpoint of the base), the angle bisector (the line segment that divides the vertex angle into two equal angles), and the perpendicular bisector of the base (the line perpendicular to the base and passing through its midpoint) are all the same line. This concurrency simplifies many geometric calculations and constructions.
3. Area Calculation:
The area of an isosceles triangle can be calculated using the standard formula for the area of a triangle:
Area = (1/2) * base * height
Where 'base' refers to the length of the base and 'height' refers to the length of the altitude from the vertex angle to the base. Alternatively, Heron's formula can be used if the lengths of all three sides are known.
4. Relationship between Angles and Sides:
The angles of an isosceles triangle are directly related to the lengths of its sides. The larger the angle, the longer the opposite side. Since the base angles are equal, the sides opposite those angles (the legs) are also equal.
Theorems Related to Isosceles Triangles
Several significant geometric theorems are directly related to isosceles triangles:
1. The Isosceles Triangle Theorem:
This theorem formally states the fundamental property mentioned earlier: If two sides of a triangle are congruent (equal in length), then the angles opposite those sides are congruent (equal in measure). This theorem is crucial for proving many other geometric relationships.
2. The Converse of the Isosceles Triangle Theorem:
The converse of this theorem is equally important: If two angles of a triangle are congruent, then the sides opposite those angles are congruent. This provides a method for determining if a triangle is isosceles by examining its angles.
3. Pythagorean Theorem (Applicable to Right Isosceles Triangles):
While the Pythagorean theorem applies to all right-angled triangles, it finds particular relevance in right isosceles triangles (45-45-90 triangles). In such a triangle, the two legs are equal, and the hypotenuse is √2 times the length of each leg. This allows for easy calculation of side lengths.
Applications of Isosceles Triangles
Isosceles triangles appear frequently in various applications across different fields:
1. Architecture and Construction:
Many architectural designs incorporate isosceles triangles. The symmetrical nature makes them aesthetically pleasing and structurally sound in roof designs, support structures, and decorative elements.
2. Engineering:
In structural engineering, the properties of isosceles triangles are utilized in the design of trusses and other load-bearing structures. Their stability and strength make them ideal for these applications.
3. Nature:
Isosceles triangles can be observed in natural formations, such as the symmetrical arrangement of leaves on certain plants or the shape of some crystals.
4. Art and Design:
The visual balance and symmetry of isosceles triangles are frequently used in art, design, and logos. Their inherent stability and pleasing visual characteristics make them a popular choice.
5. Mathematics and Geometry:
Beyond their practical applications, isosceles triangles serve as fundamental building blocks for exploring more complex geometric concepts and theorems. They are essential for understanding congruence, similarity, and trigonometric functions.
Solving Problems Involving Isosceles Triangles
Numerous geometric problems involve isosceles triangles. Solving these problems often requires using the properties and theorems discussed above, along with other geometric principles. Here's a general approach:
- Identify the given information: Determine what information is provided (side lengths, angles, altitudes, etc.).
- Identify the unknown: Determine what needs to be calculated (side lengths, angles, areas, etc.).
- Apply relevant theorems and properties: Use the isosceles triangle theorem, its converse, the Pythagorean theorem (if applicable), and other geometric principles to establish relationships between the known and unknown quantities.
- Solve the equations: Use algebraic methods to solve for the unknown quantities.
- Check your answer: Ensure that the solution is consistent with the given information and the properties of isosceles triangles.
Different Types of Isosceles Triangles
While all isosceles triangles share the defining characteristic of having two equal sides, they can be further categorized based on their angles:
- Acute Isosceles Triangle: All three angles are acute (less than 90 degrees).
- Right Isosceles Triangle: One angle is a right angle (90 degrees), and the other two angles are equal (45 degrees each).
- Obtuse Isosceles Triangle: One angle is obtuse (greater than 90 degrees), and the other two angles are acute and equal.
Conclusion
The isosceles triangle, a seemingly simple geometric figure, holds significant importance in mathematics, engineering, architecture, and other fields. Its unique properties and the theorems related to it provide powerful tools for solving geometric problems and understanding more complex geometric concepts. By understanding the defining characteristics, properties, and applications of isosceles triangles, we gain a deeper appreciation for the elegance and utility of geometry in the world around us. Mastering the concepts related to isosceles triangles forms a crucial foundation for further exploration of geometric principles and their applications in various disciplines. Remember that consistent practice and a strong understanding of fundamental geometric theorems are key to effectively solving problems related to isosceles triangles and expanding your knowledge of this fascinating area of mathematics.
Latest Posts
Latest Posts
-
Common Multiples Of 4 And 8
Mar 29, 2025
-
Are Planar And Angular Nodes The Same
Mar 29, 2025
-
Which Of The Following Is Most Accurate
Mar 29, 2025
-
Name The 3 Parts Of A Dna Nucleotide
Mar 29, 2025
-
What Would Happen If The Earths Axis Was Not Tilted
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Triangle With Two Equal Sides Is Called . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
