The Smallest Even Prime Number Is
Juapaving
Apr 01, 2025 · 5 min read
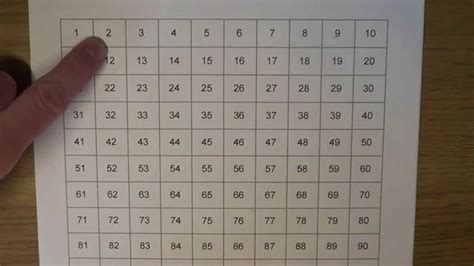
Table of Contents
The Smallest Even Prime Number Is… 2! A Deep Dive into Prime Numbers and Their Properties
The question, "What is the smallest even prime number?" might seem deceptively simple. The answer, however, opens the door to a fascinating world of number theory, exploring the fundamental building blocks of mathematics and the unique properties that define prime numbers. This article will not only answer the question definitively but also delve into the intricacies of prime numbers, their significance in mathematics and cryptography, and some of the unsolved mysteries surrounding them.
Understanding Prime Numbers
Before we definitively answer our core question, let's establish a solid understanding of what constitutes a prime number. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. This seemingly simple definition hides a wealth of complexity. Let's break it down further:
- Natural Numbers: These are the counting numbers: 1, 2, 3, 4, and so on. We exclude zero and negative numbers from our consideration of prime numbers.
- Greater than 1: The number 1 is not considered a prime number. This is a crucial point, as it forms the basis for the unique factorization theorem.
- No Positive Divisors Other Than 1 and Itself: This means that if you try to divide the prime number by any whole number other than 1 and the number itself, you'll always get a fraction or a decimal – not a whole number.
For example:
- 2 is a prime number: Its only positive divisors are 1 and 2.
- 3 is a prime number: Its only positive divisors are 1 and 3.
- 4 is not a prime number: It's divisible by 1, 2, and 4.
- 5 is a prime number: Its only positive divisors are 1 and 5.
- 6 is not a prime number: It's divisible by 1, 2, 3, and 6.
And so on. The identification of prime numbers can be surprisingly challenging, especially as the numbers get larger.
The Uniqueness of 2: The Smallest Even Prime Number
Now, we can directly address the question: The smallest even prime number is 2.
Why is this significant? It's the only even prime number. All other even numbers are divisible by 2, meaning they have at least three divisors (1, 2, and themselves), violating the definition of a prime number. This unique characteristic of 2 sets it apart and makes it a crucial element in various mathematical concepts.
The Sieve of Eratosthenes: A Method for Finding Prime Numbers
One of the oldest and simplest methods for finding prime numbers is the Sieve of Eratosthenes. This algorithm works by iteratively eliminating multiples of prime numbers. Here's how it works:
- Start with a list of natural numbers: Begin with a list of numbers starting from 2.
- Identify the smallest unmarked number: This is your next prime number.
- Mark all multiples of the prime number: Cross off all multiples of the prime number you just identified.
- Repeat: Repeat steps 2 and 3 until you've reached the desired range. The remaining unmarked numbers are your prime numbers.
Prime Numbers and the Fundamental Theorem of Arithmetic
The prime numbers are the fundamental building blocks of all whole numbers. This is formally stated in the Fundamental Theorem of Arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers, disregarding the order of the factors. This theorem is a cornerstone of number theory and is used extensively in various mathematical proofs and algorithms.
For example:
- 12 = 2 x 2 x 3
- 35 = 5 x 7
- 100 = 2 x 2 x 5 x 5
This unique factorization into prime numbers is essential in many areas of mathematics, and the understanding that 2 is the only even prime is a fundamental part of this understanding.
The Importance of Prime Numbers in Cryptography
Prime numbers play a pivotal role in modern cryptography, the science of secure communication. Many widely used encryption algorithms, such as RSA, rely on the difficulty of factoring large numbers into their prime factors. The security of these systems rests on the computational infeasibility of factoring the product of two very large prime numbers. The fact that 2 is the only even prime, while seemingly simple, contributes to the foundational understanding of the properties of these numbers and informs the development of cryptographic algorithms.
Open Questions and Unsolved Mysteries Surrounding Prime Numbers
Despite centuries of research, many mysteries surrounding prime numbers remain unsolved. Some notable open questions include:
- The Twin Prime Conjecture: Twin primes are pairs of prime numbers that differ by 2 (e.g., 3 and 5, 11 and 13). The twin prime conjecture states that there are infinitely many twin prime pairs. While substantial progress has been made, a definitive proof remains elusive.
- Goldbach's Conjecture: This conjecture proposes that every even integer greater than 2 can be expressed as the sum of two prime numbers. Again, despite extensive testing and supporting evidence, a formal proof remains elusive.
- The Riemann Hypothesis: This is one of the most important unsolved problems in mathematics. It concerns the distribution of prime numbers and has profound implications for number theory and other areas of mathematics.
These unsolved problems highlight the enduring complexity and fascination surrounding prime numbers. The seemingly simple fact that 2 is the only even prime number provides a starting point for understanding the intricacies of these fundamental mathematical objects.
Conclusion: The Significance of the Smallest Even Prime
The seemingly simple question, "What is the smallest even prime number?" leads to a rich exploration of prime numbers, their properties, and their significance in mathematics and cryptography. The unique position of 2 as the only even prime number is a fundamental fact that underpins many mathematical theorems and algorithms. Understanding this foundational concept helps to appreciate the depth and complexity of number theory and the ongoing quest to unravel the mysteries surrounding prime numbers. The journey from this simple question to the vast landscape of unsolved problems in number theory underscores the enduring power and beauty of mathematics. The seemingly simple answer – 2 – provides the key to unlocking a world of mathematical exploration and discovery, emphasizing the enduring importance of fundamental concepts in building a deeper understanding of the mathematical universe.
Latest Posts
Latest Posts
-
Plant Is Where Photosynthesis Takes Place
Apr 02, 2025
-
12 Cm Is How Many Inches
Apr 02, 2025
-
The Most Abundant Gas In The Earths Atmosphere Is
Apr 02, 2025
-
Is Rubbing Alcohol And Denatured Alcohol The Same
Apr 02, 2025
-
Is 17 A Prime Number Or A Composite Number
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about The Smallest Even Prime Number Is . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
