The Rate Of Change Of Velocity Is Called
Juapaving
Mar 31, 2025 · 6 min read
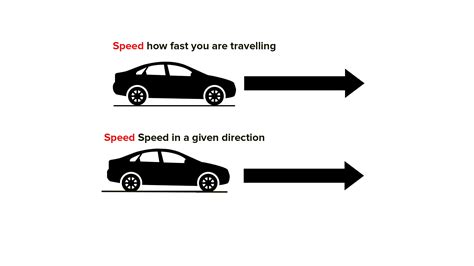
Table of Contents
The Rate of Change of Velocity is Called: Acceleration – A Deep Dive into Kinematics
The fundamental concept in physics describing how the velocity of an object changes over time is acceleration. It's a crucial element in understanding motion, and its implications reach far beyond simple calculations, impacting everything from designing rockets to understanding the orbits of planets. This article will explore acceleration in detail, covering its definition, calculation, types, applications, and the relationships it holds with other kinematic variables.
Understanding Acceleration: More Than Just Speeding Up
Many people associate acceleration solely with increasing speed. While speeding up is a form of acceleration, it's only part of the picture. Acceleration is the rate at which velocity changes. This means it encompasses not only changes in the magnitude of velocity (speed) but also changes in its direction.
Think about a car driving around a circular track at a constant speed. Even though the speed remains unchanged, the car is constantly accelerating because its direction is changing. This highlights the crucial distinction: acceleration is a vector quantity, possessing both magnitude and direction, unlike speed, which is a scalar quantity (magnitude only).
Defining Acceleration Mathematically
Mathematically, average acceleration (a<sub>avg</sub>) is defined as the change in velocity (Δv) divided by the change in time (Δt):
a<sub>avg</sub> = Δv / Δt = (v<sub>f</sub> - v<sub>i</sub>) / (t<sub>f</sub> - t<sub>i</sub>)
Where:
- a<sub>avg</sub> represents average acceleration
- v<sub>f</sub> is the final velocity
- v<sub>i</sub> is the initial velocity
- t<sub>f</sub> is the final time
- t<sub>i</sub> is the initial time
This equation provides the average acceleration over a given time interval. For instantaneous acceleration (acceleration at a specific point in time), we use calculus:
a = dv/dt
This equation represents the derivative of velocity with respect to time. It describes the acceleration at any given instant.
Types of Acceleration
Understanding the different types of acceleration is crucial for grasping the nuances of motion. These types are not mutually exclusive; an object can experience multiple types of acceleration simultaneously.
1. Uniform Acceleration (Constant Acceleration)
Uniform acceleration occurs when the acceleration remains constant over time. This simplifies calculations significantly, allowing for the use of straightforward kinematic equations. Examples include a freely falling object near the Earth's surface (neglecting air resistance) or a car accelerating at a steady rate.
2. Non-Uniform Acceleration (Variable Acceleration)
Non-uniform acceleration is characterized by a changing acceleration value over time. This is much more common in real-world scenarios. Think of a rocket launching – its acceleration changes drastically as fuel is consumed and gravitational forces vary. Analyzing non-uniform acceleration often requires more sophisticated mathematical techniques, such as calculus.
3. Positive Acceleration
Positive acceleration indicates that the velocity is increasing in the direction of motion. This is the most intuitive form of acceleration, representing speeding up.
4. Negative Acceleration (Deceleration or Retardation)
Negative acceleration means that the velocity is decreasing in the direction of motion. This is often referred to as deceleration or retardation. It signifies slowing down. Important Note: Negative acceleration doesn't necessarily mean the object is slowing down. If the object has a negative velocity and a negative acceleration, it is actually speeding up in the negative direction.
5. Centripetal Acceleration
Centripetal acceleration is the acceleration experienced by an object moving in a circular path at a constant speed. The direction of the acceleration is always towards the center of the circle. This is a crucial concept in understanding circular motion and orbital mechanics.
6. Tangential Acceleration
Tangential acceleration is the acceleration component that is parallel to the velocity vector. It signifies a change in the speed of an object moving along a curved path. This is different from centripetal acceleration which only changes the direction.
Calculating Acceleration: Practical Applications
Calculating acceleration isn't just an academic exercise; it's essential in numerous fields.
1. Automotive Engineering
Understanding acceleration is crucial for designing and testing vehicles. Engineers use acceleration data to optimize engine performance, braking systems, and overall vehicle dynamics. This includes calculating the rate at which a car can achieve specific speeds and ensuring safe stopping distances.
2. Aerospace Engineering
In aerospace, calculating acceleration is paramount for designing rockets, aircraft, and spacecraft. Accurately predicting the acceleration forces during launch, ascent, and re-entry is essential for ensuring structural integrity and astronaut safety. Understanding acceleration profiles is vital for efficient trajectory planning.
3. Physics Experiments
In physics laboratories, measuring and analyzing acceleration is a common practice. Experiments involving free fall, inclined planes, and projectile motion frequently require calculations of acceleration to validate theoretical predictions.
4. Sports Science
Sports scientists use acceleration data to analyze athletic performance. Analyzing the acceleration of athletes during sprints, jumps, or other movements helps optimize training programs and improve performance.
Acceleration and Other Kinematic Variables: A Connected System
Acceleration is intricately linked to other kinematic variables: displacement, velocity, and time. These variables are interconnected through several important equations, known as the equations of motion or kinematic equations. These equations allow us to calculate unknown variables if we know others. The specific equations used depend on whether the acceleration is uniform or non-uniform. For uniform acceleration, the commonly used equations include:
- v = u + at (final velocity = initial velocity + acceleration × time)
- s = ut + ½at² (displacement = initial velocity × time + ½ × acceleration × time²)
- v² = u² + 2as (final velocity² = initial velocity² + 2 × acceleration × displacement)
- s = ½(u + v)t (displacement = ½ × (initial velocity + final velocity) × time)
Where:
- v represents final velocity
- u represents initial velocity
- a represents acceleration
- t represents time
- s represents displacement
Beyond the Basics: Advanced Concepts Related to Acceleration
While the fundamental definition and calculations of acceleration are relatively straightforward, several more advanced concepts build upon this foundation:
-
Jerk: The rate of change of acceleration is called jerk. It's a measure of the "smoothness" or "roughness" of acceleration. High jerk values can be uncomfortable or even dangerous, as they indicate rapid changes in acceleration. Jerk is important in the design of vehicles and amusement park rides, where smooth transitions are desired.
-
Relativistic Acceleration: In Einstein's theory of special relativity, acceleration is treated differently than in Newtonian mechanics, especially at speeds approaching the speed of light. At these high speeds, the mass of an object increases, making it increasingly difficult to accelerate.
-
Acceleration in Different Frames of Reference: The measured acceleration of an object depends on the frame of reference from which it is observed. This concept is vital in understanding relative motion and the principles of relativity.
-
Non-inertial Frames of Reference: In non-inertial frames of reference (accelerating frames), fictitious forces, such as the centrifugal force, appear to act on objects. Understanding these fictitious forces is crucial for analyzing motion in rotating frames or accelerating vehicles.
Conclusion: The Ubiquitous Nature of Acceleration
The rate of change of velocity, acceleration, is a fundamental concept in physics with wide-ranging applications. From understanding the motion of everyday objects to designing complex machinery and spacecraft, a thorough grasp of acceleration is essential. This article has explored the various facets of acceleration, from its basic definition and calculation to its advanced applications and relationship with other kinematic variables. By understanding acceleration's nuances and its connection to other physical principles, we gain a more profound understanding of the world around us and the universe beyond. Whether you're a student learning about motion for the first time or a professional working in a field related to mechanics, the significance of acceleration remains undeniable.
Latest Posts
Latest Posts
-
What Are The Factors Of 94
Apr 01, 2025
-
Can You Have A Negative Acceleration
Apr 01, 2025
-
What Is The Square Root 69
Apr 01, 2025
-
Difference Between Communicable And Non Communicable Disease
Apr 01, 2025
-
How To Increase The Strength Of A Magnetic Field
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about The Rate Of Change Of Velocity Is Called . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
