The Point At Which The Medians Intersect In A Triangle
Juapaving
Mar 24, 2025 · 6 min read
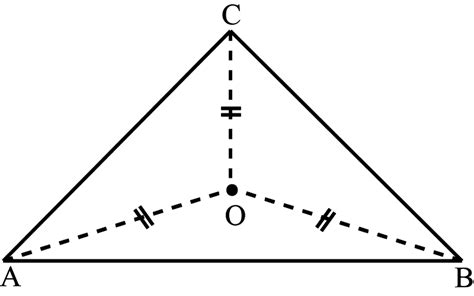
Table of Contents
- The Point At Which The Medians Intersect In A Triangle
- Table of Contents
- The Point Where Medians Intersect: Exploring the Centroid of a Triangle
- Understanding Medians and Their Intersection
- Constructing Medians
- The Significance of the Centroid
- Key Properties of the Centroid
- Mathematical Derivations and Proofs
- Proof: 2:1 Ratio of Median Division
- Proof: Center of Mass
- Applications of the Centroid
- Engineering and Physics
- Computer Graphics and Computer-Aided Design (CAD)
- Statistics and Data Analysis
- Beyond the Basic Triangle: Exploring Extensions
- Conclusion: The Underrated Power of the Centroid
- Latest Posts
- Latest Posts
- Related Post
The Point Where Medians Intersect: Exploring the Centroid of a Triangle
The humble triangle, a fundamental shape in geometry, holds within its seemingly simple structure a wealth of fascinating properties. One such property centers around the intersection of its medians – lines drawn from each vertex to the midpoint of the opposite side. This point of intersection, known as the centroid, is far more significant than it might initially appear. This article delves deep into the centroid's properties, its mathematical significance, and its applications across various fields.
Understanding Medians and Their Intersection
Before exploring the centroid's characteristics, let's establish a solid understanding of medians. A median of a triangle is a line segment joining a vertex to the midpoint of the opposite side. Every triangle possesses three medians, one from each vertex. Crucially, these three medians are not just random lines; they always intersect at a single point – the centroid.
Constructing Medians
To visualize this, imagine a triangle ABC. Let's denote the midpoints of sides AB, BC, and AC as D, E, and F respectively. Then, the line segments AD, BE, and CF are the medians of triangle ABC. Constructing these medians using a ruler and compass, or even utilizing geometry software, will clearly demonstrate their concurrent intersection.
The Significance of the Centroid
The point of intersection of these three medians isn't just an arbitrary point; it's the centroid of the triangle, often denoted by G. This point holds several remarkable properties, making it a crucial element in geometry and beyond.
Key Properties of the Centroid
The centroid boasts a unique set of properties that distinguish it from other points within a triangle:
-
Dividing Medians in a 2:1 Ratio: This is perhaps the most well-known property of the centroid. The centroid divides each median into a ratio of 2:1. More precisely, the distance from a vertex to the centroid is twice the distance from the centroid to the midpoint of the opposite side. This means that the centroid is located two-thirds of the way along each median from the corresponding vertex.
-
Center of Mass: The centroid represents the center of mass of a triangle. If the triangle were a thin, uniform lamina (a flat surface with negligible thickness), the centroid would be the point at which the triangle would perfectly balance. This property has significant applications in physics and engineering.
-
Geometric Mean: The centroid is also related to the geometric mean of the vertices. Consider the vertices of the triangle as points in a coordinate system. The centroid's coordinates are simply the average of the coordinates of the vertices. This property is immensely useful in computational geometry.
-
Intersection of other Concurrent Lines: While medians are the most commonly associated lines intersecting at the centroid, it's noteworthy that other sets of concurrent lines within a triangle also pass through the centroid under certain circumstances. This involves more complex geometrical relationships and explores the centroid's role within a broader network of lines within the triangle.
Mathematical Derivations and Proofs
Let's delve into the mathematical proofs supporting these claims. While rigorous proofs often require vector calculus or coordinate geometry, a simpler approach can provide intuition.
Proof: 2:1 Ratio of Median Division
Consider triangle ABC with medians AD, BE, and CF intersecting at centroid G. Using vector methods, we can represent the position vector of the centroid G as the average of the position vectors of the vertices A, B, and C. From this, it’s relatively straightforward to demonstrate that the ratio AG:GD is 2:1. A similar approach can be applied to the other medians.
Proof: Center of Mass
Imagine the triangle as a collection of infinitesimally small masses distributed uniformly across its area. By considering the moments of these masses about the x and y axes, it can be shown that the centroid's coordinates represent the center of mass – the point where the weighted average of all these tiny masses lies.
Applications of the Centroid
The centroid's properties make it invaluable in several applications:
Engineering and Physics
-
Structural Design: In engineering, understanding the centroid is crucial for determining the center of gravity of structures, essential for stability and load calculations. Bridges, buildings, and other structures rely on accurate centroid calculations to ensure their structural integrity.
-
Robotics: In robotics, the centroid plays a vital role in controlling robot movements and balancing. Understanding the centroid helps in designing robots that can maintain balance and perform complex maneuvers.
-
Aerospace Engineering: The concept of the center of mass, directly related to the centroid, is fundamental in aerospace engineering for aircraft design and flight stability. The centroid's position influences the aircraft's balance and its response to forces.
Computer Graphics and Computer-Aided Design (CAD)
-
Image Processing: Centroid calculations are used in image processing to locate the center of objects in images. This is vital for various applications, including object recognition and image analysis.
-
3D Modeling: In 3D modeling, the centroid is essential for manipulating and transforming 3D objects. Understanding the centroid facilitates tasks such as rotation, scaling, and translation of complex shapes.
-
Game Development: Centroid calculations are used in game development for tasks such as character animation, collision detection, and physics simulation. Accurate centroid computation is critical for creating realistic and believable game worlds.
Statistics and Data Analysis
-
Data Visualization: The centroid, representing the average of a set of data points, is used in data visualization to represent the center of a dataset. This is crucial for understanding the distribution and characteristics of data.
-
Clustering: In clustering algorithms, the centroid represents the center of a cluster of data points. This helps in grouping similar data points together and identifying patterns.
Beyond the Basic Triangle: Exploring Extensions
The concept of the centroid isn't limited to simple triangles. It extends to other geometric shapes and even to more complex mathematical structures:
-
Tetrahedrons and Higher Dimensions: The centroid concept generalizes to higher dimensions. For example, a tetrahedron (a four-sided solid) also possesses a centroid, which is the average of its four vertices. This generalizes to n-dimensional simplices.
-
Irregular Shapes: While the calculation is more complex, the centroid can also be found for irregular shapes using integration techniques. This extends the usefulness of the centroid to a wider range of real-world applications.
-
Weighted Centroids: The concept can be expanded to incorporate weighted centroids, where different parts of the shape or data points have different weights. This is particularly useful in situations where certain points or regions are more significant than others.
Conclusion: The Underrated Power of the Centroid
The centroid, the intersection point of a triangle's medians, is far more than just a geometric curiosity. Its properties are fundamental to various fields, showcasing the deep interplay between geometry, physics, computer science, and statistics. From ensuring structural stability in engineering to enabling realistic animations in game development, the centroid's impact is widespread and often understated. A thorough understanding of this seemingly simple concept unveils a world of applications and mathematical elegance. This exploration only scratches the surface of the centroid's significance, inviting further investigation into its rich mathematical properties and diverse real-world implementations. The centroid stands as a testament to the power of fundamental geometrical concepts and their unexpected influence across diverse scientific and technological disciplines.
Latest Posts
Latest Posts
-
Common Multiples Of 7 And 3
Mar 27, 2025
-
Why Were The Prokaryotes Split Into Two Kingdoms
Mar 27, 2025
-
500 Yards Is How Many Feet
Mar 27, 2025
-
What Is The Unit For Acceleration
Mar 27, 2025
-
Which Of The Following Is Not A Function Of Kidneys
Mar 27, 2025
Related Post
Thank you for visiting our website which covers about The Point At Which The Medians Intersect In A Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
