Similarities Between A Square And A Rhombus
Juapaving
Mar 31, 2025 · 6 min read
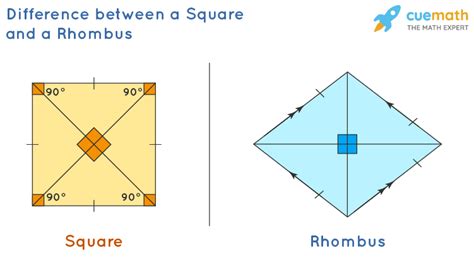
Table of Contents
Delving Deep: Unveiling the Striking Similarities Between Squares and Rhombuses
Squares and rhombuses, both captivating shapes found within the realm of geometry, often spark confusion due to their shared characteristics. While distinct in certain aspects, understanding their similarities is crucial for grasping fundamental geometric concepts. This comprehensive exploration will delve into the fascinating world of squares and rhombuses, highlighting their shared attributes and clarifying the subtle differences that set them apart. We'll explore their properties, delve into their applications, and touch upon the mathematical elegance that connects these two seemingly simple figures.
Key Similarities: Where Squares and Rhombuses Converge
At first glance, a square and a rhombus might appear quite different. However, a closer examination reveals a surprising number of shared attributes. These similarities form the foundation of their geometric relationship, demonstrating a clear hierarchical connection within the broader family of quadrilaterals.
1. All Sides Are Equal: The Defining Characteristic
The most prominent similarity between a square and a rhombus lies in their sides. Both shapes possess four sides of equal length. This fundamental characteristic is paramount in their classification. This means that if you measure the length of each side of a square, you will find they are all identical. The same principle holds true for a rhombus. This shared property immediately categorizes them both as a subset of quadrilaterals known as parallelograms.
2. Opposite Sides Are Parallel: A Parallelogram Property
Both squares and rhombuses are special types of parallelograms. A parallelogram is defined as a quadrilateral with opposite sides that are parallel and equal in length. This property naturally follows from the equal-sides characteristic mentioned above. Because all four sides of a square and a rhombus are equal, their opposite sides are inherently parallel. This parallelism leads to several other interesting geometric consequences, as we will explore later.
3. Opposite Angles Are Equal: Symmetry in Action
Another significant similarity is the equality of opposite angles. In both squares and rhombuses, opposite angles are congruent (equal in measure). This property is a direct consequence of their parallel sides. The angles formed by the intersection of parallel lines and transversals (the sides of the shape) maintain a specific relationship, resulting in the equality of opposite angles. This symmetry contributes to the overall balanced aesthetic of both shapes.
4. Diagonals Bisect Each Other: A Shared Intersection Property
Both squares and rhombuses share a crucial characteristic regarding their diagonals. The diagonals of both shapes bisect each other. This means that the diagonals intersect at their midpoints, dividing each diagonal into two equal segments. This intersection point serves as a center of symmetry for both shapes. This property is inherent to all parallelograms, and thus naturally extends to both squares and rhombuses.
5. Area Calculation Similarity: A Shared Formula Base
While the specific formulas differ, both the area of a square and the area of a rhombus can be derived from the concept of base and height. A square's area is simply side * side, which can be viewed as base * height (since all sides are equal and perpendicular). The rhombus's area utilizes a similar principle, albeit with a slightly more complex formula: base * height. The height in a rhombus refers to the perpendicular distance between opposite sides (or parallel sides). This commonality in approaching area calculation highlights the underlying geometric similarities.
Where They Diverge: Distinguishing Squares from Rhombuses
Despite their numerous shared attributes, there are crucial differences that set squares and rhombuses apart. These distinguishing features clarify their unique identities within the broader geometric landscape.
1. Angle Measurement: The Defining Distinction
The most significant difference between a square and a rhombus lies in their angles. A square is a special type of rhombus where all four angles are right angles (90 degrees). A rhombus, on the other hand, only requires that opposite angles be equal; its angles are not necessarily right angles. This means a rhombus can be "tilted" or "skewed," while a square remains perfectly upright. This difference is fundamental and forms the basis for their distinct classifications.
2. Diagonal Lengths: A Metric for Differentiation
Another key distinction lies in the lengths of their diagonals. In a square, the diagonals are equal in length and perpendicular to each other. This is a direct consequence of the right angles present in a square. In a rhombus, while the diagonals still bisect each other, they are not necessarily equal in length, and they are not always perpendicular. This difference in diagonal lengths provides a clear visual and metric means to distinguish between the two shapes.
3. Symmetry Properties: A Deeper Geometric Analysis
While both possess certain symmetries, the level and type of symmetry differ. A square exhibits a higher degree of symmetry. It possesses both rotational symmetry (90°, 180°, 270°) and reflectional symmetry (across both diagonals and horizontal/vertical axes). A rhombus possesses reflectional symmetry across its diagonals, but its rotational symmetry is limited to 180°. This difference in symmetry reflects the more constrained structure of the rhombus compared to the highly symmetrical square.
Applications and Real-World Examples
The geometric properties of squares and rhombuses find numerous applications in various fields, ranging from architecture and engineering to design and art.
Squares in Architecture and Design:
- Building foundations: Squares provide stability and are frequently used in building foundations and structural designs.
- Tiles and paving: Square tiles are commonly used for flooring, walls, and paving due to their efficient space-filling properties.
- Window and door frames: Square frames are common due to their structural strength and aesthetic appeal.
Rhombuses in Architecture and Design:
- Roof structures: Rhombus shapes can be found in certain roof structures, offering efficient support and visually striking designs.
- Lattice structures: The properties of rhombuses are utilized in creating strong and lightweight lattice structures.
- Tessellations: Rhombuses, especially when combined in various arrangements, can create complex and attractive tessellations (patterns that cover a plane without gaps or overlaps). These can be found in art, tilework, and even in some natural formations.
Both Shapes in Art and Design:
- Geometric art: Both squares and rhombuses are frequently employed in geometric art, contributing to the visual balance and symmetry of the artwork.
- Logo design: The clean lines and geometric precision of both shapes make them popular choices for logo design, signifying stability, strength, or precision.
- Pattern creation: The combination of squares and rhombuses can create intricate and visually engaging patterns in textiles, wallpapers, and various decorative applications.
Conclusion: A Unified Geometric Perspective
This in-depth analysis reveals the fascinating interplay between squares and rhombuses. While distinct in certain aspects—particularly in their angle measurements and diagonal properties—their shared characteristics solidify their close relationship within the family of quadrilaterals. Understanding their similarities and differences not only enhances one's geometric knowledge but also provides valuable insights into the applications of these shapes across diverse disciplines. From the foundational stability of a square-based building to the elegant tessellations created using rhombuses, these seemingly simple shapes contribute significantly to our understanding and appreciation of the visual and structural world around us. The intricate details of their geometry underscore the power and elegance of mathematical principles, offering a glimpse into the beauty and harmony found within the abstract world of shapes.
Latest Posts
Latest Posts
-
What Is The Ocean Between North America And Europe
Apr 02, 2025
-
How Are Compounds And Mixtures Alike
Apr 02, 2025
-
A Man Stands 10 M In Front
Apr 02, 2025
-
Round 972381 89348 To The Nearest Thousand
Apr 02, 2025
-
Letters With A Line Of Symmetry
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Similarities Between A Square And A Rhombus . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
