Rectangular Equation To Polar Form Calculator
Juapaving
Mar 24, 2025 · 6 min read
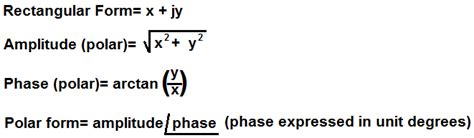
Table of Contents
From Rectangular to Polar: A Comprehensive Guide with Calculator Insights
Converting equations from rectangular coordinates (x, y) to polar coordinates (r, θ) is a fundamental concept in mathematics, particularly useful in fields like physics, engineering, and computer graphics. This transformation allows us to represent the same geometric relationship using a different coordinate system, often simplifying calculations or providing a more intuitive representation. This article delves into the intricacies of this conversion, exploring the underlying formulas, providing a step-by-step process, and discussing the practical implications of using a rectangular equation to polar form calculator.
Understanding Rectangular and Polar Coordinate Systems
Before diving into the conversion process, it's crucial to understand the two coordinate systems involved:
Rectangular Coordinates (x, y)
This is the familiar Cartesian coordinate system, where a point is uniquely identified by its horizontal distance (x-coordinate) from the y-axis and its vertical distance (y-coordinate) from the x-axis. The x and y axes intersect at the origin (0, 0).
Polar Coordinates (r, θ)
In the polar coordinate system, a point is defined by its distance (r) from the origin (also called the pole) and the angle (θ) it makes with the positive x-axis, measured counterclockwise. The distance 'r' is always non-negative, and the angle 'θ' is typically expressed in radians or degrees.
The Conversion Formulas: Bridging Rectangular and Polar
The core of converting a rectangular equation to its polar equivalent lies in the following fundamental relationships:
- x = r cos θ
- y = r sin θ
- r² = x² + y²
- tan θ = y/x (provided x ≠ 0)
These formulas provide the mathematical bridge between the two coordinate systems. We use them to substitute x and y in the rectangular equation with their polar equivalents, resulting in a polar equation expressed in terms of r and θ.
Step-by-Step Guide: Converting Rectangular Equations to Polar Form
Let's illustrate the conversion process with a step-by-step example. Consider the rectangular equation:
x² + y² = 25
This represents a circle with a radius of 5 centered at the origin. Let's convert it to polar form:
-
Substitute: Using the relationship r² = x² + y², we can directly substitute:
r² = 25
-
Solve for r: Taking the square root of both sides, we get:
r = ±5
Since 'r' represents distance, we only consider the positive solution:
r = 5
This polar equation, r = 5, concisely represents the same circle. Note that the angle θ is not explicitly present, indicating that the distance from the origin (r) remains constant regardless of the angle.
More Complex Conversions: Handling Various Equation Types
The conversion process becomes more involved with more complex rectangular equations. Let's examine an example involving a line:
y = 2x + 1
-
Substitute: Replace 'x' and 'y' with their polar equivalents:
r sin θ = 2(r cos θ) + 1
-
Solve for r: Our goal is to express 'r' in terms of θ. Let's rearrange the equation:
r sin θ - 2r cos θ = 1 r(sin θ - 2 cos θ) = 1 r = 1 / (sin θ - 2 cos θ)
This is the polar form of the equation y = 2x + 1. Notice how the polar equation expresses the distance 'r' as a function of the angle θ.
The Role of a Rectangular Equation to Polar Form Calculator
While manual conversion is essential for understanding the process, a rectangular equation to polar form calculator can be invaluable, especially when dealing with intricate equations. These calculators automate the conversion process, saving time and reducing the risk of errors.
Benefits of Using a Calculator:
- Speed and Efficiency: Calculators significantly reduce the time required for conversion, allowing you to focus on interpreting the results rather than getting bogged down in calculations.
- Accuracy: Manual calculations are prone to errors, especially with more complex equations. A calculator minimizes the chance of such errors, ensuring accurate results.
- Handling Complex Equations: Calculators can easily handle equations that are too complex or tedious for manual conversion, providing quick and reliable solutions.
- Exploration and Visualization: Calculators can often be coupled with graphing tools, enabling you to visualize both the rectangular and polar representations of the equation, offering a deeper understanding of the transformation.
Features to Look For in a Calculator:
- Input Flexibility: The calculator should be able to accept a wide variety of input formats for rectangular equations.
- Step-by-Step Solutions: Some calculators provide step-by-step solutions, allowing you to follow the conversion process and enhance your understanding.
- Output Clarity: The polar equation should be presented clearly and accurately.
- Graphical Representation: Integration with graphing capabilities can significantly aid in understanding the transformed equation.
Applications of Polar Coordinates: Real-World Examples
The conversion from rectangular to polar coordinates is not merely a mathematical exercise; it finds extensive application in various fields:
- Physics: Polar coordinates are indispensable in analyzing motion in circular paths, projectile motion, and wave phenomena. The symmetry inherent in many physical systems often makes polar coordinates more convenient than rectangular coordinates.
- Engineering: In robotics and mechanical engineering, polar coordinates simplify the description of robotic arm movements and the design of mechanisms with rotational components.
- Computer Graphics: Polar coordinates are crucial for creating circular or spiral shapes, designing radial gradients, and implementing transformations in computer graphics and game development.
- Navigation: GPS systems, radar, and sonar rely heavily on polar coordinates to determine the location and direction of objects relative to a central point.
- Astronomy: The positions of celestial bodies are often described using polar coordinates, making calculations of orbital mechanics and astronomical observations more straightforward.
Beyond the Basics: Advanced Conversion Techniques
While the basic conversion formulas suffice for many cases, more complex scenarios might require advanced techniques:
- Implicit Equations: Converting implicit equations (where x and y are not explicitly expressed as functions of each other) can be challenging and may require specialized techniques or the use of advanced calculators.
- Parametric Equations: When dealing with parametric equations (where x and y are defined as functions of a third parameter, such as t), the conversion to polar form requires substituting the parametric expressions for x and y into the polar conversion formulas and then eliminating the parameter 't' if possible.
Conclusion: Mastering the Transformation
Converting rectangular equations to polar form is a crucial skill in mathematics and various scientific and engineering disciplines. Understanding the underlying principles, the step-by-step conversion process, and leveraging the capabilities of a rectangular equation to polar form calculator empowers you to tackle this transformation with confidence and efficiency. By appreciating the benefits of both coordinate systems and choosing the most appropriate one for a given problem, you can significantly simplify calculations and gain a deeper understanding of the underlying geometric relationships. Remember that the choice of coordinate system often significantly impacts the complexity and elegance of solutions. Embrace the power of transformation!
Latest Posts
Latest Posts
-
Where Is The Circumcenter Of A Right Triangle Located
Mar 30, 2025
-
A Horizontal Row On The Periodic Table Is Called
Mar 30, 2025
-
Quotient Of 80 Divided By 5
Mar 30, 2025
-
How To Convert From Mol To Grams
Mar 30, 2025
-
What Does A Worm Heart Look Like
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Rectangular Equation To Polar Form Calculator . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
