Moment Of Inertia Of Sphere Derivation
Juapaving
Mar 27, 2025 · 5 min read
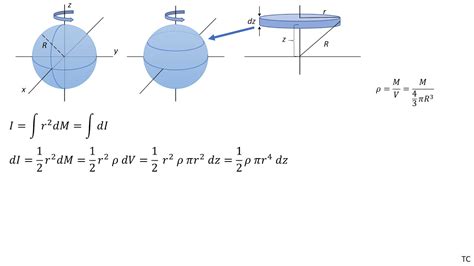
Table of Contents
Moment of Inertia of a Sphere: A Comprehensive Derivation
The moment of inertia, a crucial concept in physics and engineering, quantifies an object's resistance to changes in its rotation. Understanding its derivation, particularly for a sphere, is fundamental to analyzing rotational motion. This article provides a detailed, step-by-step derivation of the moment of inertia for a solid sphere, explaining the underlying principles and mathematical techniques involved. We'll explore different approaches and highlight the significance of this crucial physical quantity.
Understanding the Concept of Moment of Inertia
Before delving into the derivation, let's establish a firm grasp of the concept itself. The moment of inertia (I) represents the rotational analog of mass in linear motion. While mass resists changes in linear velocity, the moment of inertia resists changes in angular velocity. The greater the moment of inertia, the more difficult it is to accelerate or decelerate a rotating object.
This resistance depends on two factors:
- Mass (m): The more massive an object, the greater its resistance to changes in rotation.
- Distribution of Mass (r): The distribution of mass relative to the axis of rotation is crucial. Mass concentrated further from the axis contributes more significantly to the moment of inertia than mass closer to the axis.
Mathematically, the moment of inertia is defined as the sum of the products of each particle's mass and the square of its distance from the axis of rotation:
I = Σ mᵢrᵢ²
where:
- I is the moment of inertia
- mᵢ is the mass of the i-th particle
- rᵢ is the distance of the i-th particle from the axis of rotation
For continuous mass distributions, like a solid sphere, the summation becomes an integral:
I = ∫ r² dm
Deriving the Moment of Inertia of a Solid Sphere: Method 1 (Integration in Spherical Coordinates)
This method leverages the power of integral calculus and spherical coordinates to elegantly derive the moment of inertia. We consider a solid sphere of radius R and uniform density ρ.
1. Defining the infinitesimal mass (dm):
We begin by considering a thin spherical shell of radius r and thickness dr within the sphere. The volume of this shell is approximately 4πr²dr. Since density (ρ) is mass per unit volume, the mass of this shell (dm) is:
dm = ρ(4πr²dr)
2. Defining the distance from the axis of rotation:
For an axis passing through the sphere's center, the distance of each mass element (dm) from the axis is simply r.
3. Setting up the integral:
Substituting dm into the integral for the moment of inertia:
I = ∫ r² dm = ∫₀ᴿ r² (ρ4πr²dr)
4. Evaluating the integral:
Since ρ is constant, we can pull it out of the integral:
I = 4πρ ∫₀ᴿ r⁴ dr
Solving the integral:
I = 4πρ [r⁵/5]₀ᴿ = (4πρR⁵)/5
5. Expressing the result in terms of mass:
The total mass (M) of the sphere is given by:
M = ρ(4πR³/3)
Solving for ρ:
ρ = (3M)/(4πR³)
Substituting this expression for ρ back into the equation for I:
I = [(4πR⁵)/5] * [(3M)/(4πR³)] = (2/5)MR²
Therefore, the moment of inertia of a solid sphere about an axis passing through its center is (2/5)MR².
Deriving the Moment of Inertia of a Solid Sphere: Method 2 (Integration in Cylindrical Coordinates)
This approach uses cylindrical coordinates, offering a slightly different perspective on the problem.
1. Defining the infinitesimal mass (dm):
Consider a thin cylindrical shell of radius r, height dz, and thickness dr within the sphere. The volume of this element is 2πr dr dz. The mass of this element (dm) is:
dm = ρ(2πr dr dz)
2. Defining the distance from the axis of rotation:
The distance of each mass element (dm) from the axis of rotation passing through the center of the sphere is simply r.
3. Defining the limits of integration:
The limits of integration for r are from 0 to √(R² - z²), representing the radius of the sphere at a given height z. The limits for z are from -R to R.
4. Setting up the integral:
The moment of inertia is given by:
I = ∫∫ r² dm = ∫₋ᴿᴿ ∫₀^(√(R²-z²)) r² ρ(2πr dr dz)
5. Evaluating the integral:
This double integral is more complex but can be solved using standard techniques:
First, integrate with respect to r:
∫₀^(√(R²-z²)) 2πρr³ dr = (πρ/2)(R² - z²)²
Then, integrate with respect to z:
I = πρ ∫₋ᴿᴿ (R² - z²)² dz = (8πρR⁵)/15
6. Expressing the result in terms of mass:
Using the relationship M = (4πρR³/3), we again arrive at:
I = (2/5)MR²
Significance of the Moment of Inertia of a Sphere
The moment of inertia of a sphere is a fundamental parameter in numerous applications, including:
-
Astronomy: Understanding the rotation of planets and stars. Their moments of inertia influence their rotational dynamics and affect their gravitational interactions.
-
Engineering: Designing rotating machinery like flywheels, gyroscopes, and turbines. The moment of inertia is critical for optimizing their performance and stability.
-
Physics: Analyzing the motion of rolling objects. The moment of inertia plays a crucial role in determining the kinetic energy of a rolling sphere and its acceleration down an incline.
-
Sports Science: Analyzing the motion of sports equipment like balls (baseball, soccer, bowling). The moment of inertia influences how these objects spin and react to forces.
Conclusion
The derivation of the moment of inertia for a solid sphere, though mathematically intensive, demonstrates the elegant application of integral calculus to solve problems in physics. Both methods presented – using spherical and cylindrical coordinates – provide valuable insights into the problem's structure and highlight the importance of selecting the appropriate coordinate system based on the geometry of the object and axis of rotation. Understanding this fundamental concept opens doors to a deeper appreciation of rotational mechanics and its wide-ranging applications across various scientific and engineering disciplines. The result, (2/5)MR², is a cornerstone equation in physics, regularly used in advanced calculations involving rotational dynamics. Remember, the accuracy of this derivation depends on assuming a uniform density throughout the sphere. Non-uniform density would require a more complex integration considering density as a function of position.
Latest Posts
Latest Posts
-
Lowest Common Multiple Of 9 And 10
Mar 30, 2025
-
In What Cell Organelle Does Cellular Respiration Occur
Mar 30, 2025
-
Is The Square Root Of 32 A Rational Number
Mar 30, 2025
-
Which Functional Group Is Found In Methanol
Mar 30, 2025
-
37 Degrees C Is What In Fahrenheit
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Moment Of Inertia Of Sphere Derivation . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
