Moment Of Inertia Of An Ellipse
Juapaving
Mar 29, 2025 · 6 min read
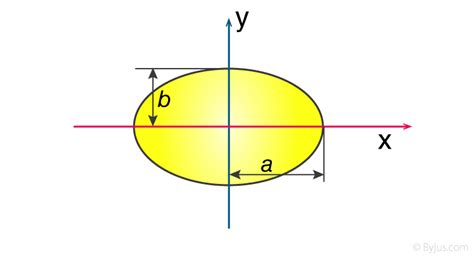
Table of Contents
Moment of Inertia of an Ellipse: A Comprehensive Guide
The moment of inertia, a crucial concept in physics and engineering, describes an object's resistance to changes in its rotation. Understanding the moment of inertia is vital for analyzing rotational motion, calculating angular momentum, and designing rotating machinery. This comprehensive guide delves into the intricacies of calculating the moment of inertia of an ellipse, exploring different approaches and applications.
Understanding Moment of Inertia
Before tackling the ellipse specifically, let's establish a firm grasp of the fundamental concept. The moment of inertia (often denoted as I) represents the rotational equivalent of mass in linear motion. While mass resists changes in linear velocity, the moment of inertia resists changes in angular velocity. Its value depends on both the object's mass distribution and the axis of rotation. A larger moment of inertia indicates a greater resistance to rotational acceleration.
The formula for the moment of inertia of a point mass m at a distance r from the axis of rotation is simply:
I = mr²
For extended objects, like an ellipse, we need to integrate over the entire mass distribution. This involves considering infinitesimal mass elements, their distances from the axis of rotation, and summing their contributions. The specific approach depends on the chosen axis of rotation.
Calculating the Moment of Inertia of an Ellipse
Calculating the moment of inertia of an ellipse presents a more complex challenge compared to simpler shapes like a circle or a rectangle. This complexity arises because the mass distribution isn't uniform along a single radius. We need to consider the varying distances of infinitesimal mass elements from the axis of rotation. The approach typically involves double integration.
Moment of Inertia about the Major Axis
Let's consider an ellipse with semi-major axis a and semi-minor axis b. We'll first calculate the moment of inertia around the major axis (the longer axis).
We start by dividing the ellipse into infinitesimal rectangular strips parallel to the minor axis. The area of each strip is approximately dA = 2y dx, where y is the height of the strip at a distance x from the center. The equation of an ellipse is:
(x²/a²) + (y²/b²) = 1
Solving for y, we get:
y = b√(1 - (x²/a²))
The area of the strip becomes:
dA = 2b√(1 - (x²/a²)) dx
Assuming a uniform mass density ρ (mass per unit area), the mass of the strip is:
dm = ρ dA = 2ρb√(1 - (x²/a²)) dx
The moment of inertia of this strip about the major axis is:
dI = dm * x² = 2ρb x²√(1 - (x²/a²)) dx
To find the total moment of inertia, we integrate over the entire ellipse (-a to a):
I_major = ∫(from -a to a) 2ρb x²√(1 - (x²/a²)) dx
This integral can be solved using a substitution method (e.g., substituting x = a sin θ), leading to the solution:
I_major = (π/4)ρab³
Since the total mass M of the ellipse is M = πabρ, we can express the moment of inertia in terms of mass:
**I_major = (1/4)M b²**
Moment of Inertia about the Minor Axis
The process for calculating the moment of inertia about the minor axis (the shorter axis) follows a similar approach. However, we now divide the ellipse into strips parallel to the major axis and integrate along the y-axis. After a similar integration process, we arrive at:
I_minor = (π/4)ρa³b
Expressing this in terms of mass:
**I_minor = (1/4)M a²**
Moment of Inertia about an Axis Through the Center Perpendicular to the Plane
For the moment of inertia about an axis perpendicular to the plane of the ellipse and passing through its center, we can apply the perpendicular axis theorem. This theorem states that the sum of the moments of inertia about any two perpendicular axes in the plane is equal to the moment of inertia about an axis perpendicular to the plane and passing through the intersection of the two axes. Therefore:
I_z = I_major + I_minor = (1/4)M(a² + b²)
Where I_z represents the moment of inertia about the z-axis.
Parallel Axis Theorem
The parallel axis theorem is incredibly useful for calculating the moment of inertia about an axis parallel to an axis passing through the center of mass. It states that the moment of inertia about an axis parallel to and a distance d from an axis through the center of mass is:
I = I_cm + Md²
Where:
- I is the moment of inertia about the parallel axis
- I_cm is the moment of inertia about the axis through the center of mass
- M is the total mass
- d is the distance between the axes
This theorem simplifies calculations significantly when dealing with axes that don't pass through the center of mass.
Applications of Moment of Inertia of an Ellipse
Understanding the moment of inertia of an ellipse has numerous applications across various fields:
Engineering Design
-
Rotating Machinery: Designing flywheels, gears, and other rotating components requires precise calculations of moment of inertia to ensure stability and efficiency. The elliptical shape, offering a unique mass distribution, might be advantageous in specific applications.
-
Structural Analysis: In structural engineering, the moment of inertia is critical for calculating the stiffness and resistance of beams and other structural elements under bending loads. Elliptical cross-sections can be used in certain structural designs.
Physics and Astronomy
-
Planetary Motion: While planets aren't perfectly elliptical, understanding the moment of inertia of an ellipse is crucial for modeling their rotational dynamics and predicting their behavior.
-
Satellite Stability: The moment of inertia plays a role in the stability and orientation of artificial satellites.
Other Applications
-
Optics: In the design of elliptical mirrors and lenses, understanding the mass distribution is relevant for calculations related to stability and manufacturing.
-
Robotics: The design of robotic arms and manipulators involves careful consideration of moment of inertia for optimal control and movement.
Conclusion
The moment of inertia of an ellipse, while seemingly a niche concept, underpins many critical calculations in diverse fields. Mastering its calculation, along with the parallel axis theorem, empowers engineers and physicists to analyze and design systems involving rotating objects, predict their behavior, and optimize performance. While the integration involved might seem daunting, understanding the underlying principles and applying the appropriate techniques leads to precise and crucial results. This detailed explanation should provide a comprehensive foundation for further exploration and application of this important concept. Remember to always consider the specific axis of rotation and the distribution of mass within the elliptical object. The equations provided here are the foundation upon which more complex analyses can be built.
Latest Posts
Latest Posts
-
What Is 35 Cm In Inches
Mar 31, 2025
-
How Many Feet In 44 Inches
Mar 31, 2025
-
What Is The Difference Between An Ecosystem And An Environment
Mar 31, 2025
-
What Are The Prime Numbers Between 20 And 30
Mar 31, 2025
-
What Is 30 As A Decimal
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Moment Of Inertia Of An Ellipse . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
