Line Of Best Fit Equation Calculator
Juapaving
Mar 26, 2025 · 6 min read
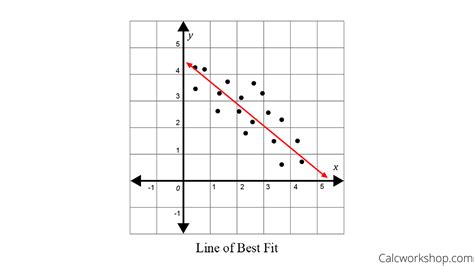
Table of Contents
Line of Best Fit Equation Calculator: A Comprehensive Guide
Finding the line of best fit, also known as the regression line, is a crucial task in statistical analysis and data visualization. It allows us to model the relationship between two variables and make predictions based on that relationship. While manual calculation is possible, it's time-consuming and prone to errors. This is where a line of best fit equation calculator becomes invaluable. This comprehensive guide will explore the concept of the line of best fit, the various methods for calculating it, and the importance of using a calculator for accurate and efficient results. We'll also delve into practical applications and address common questions.
Understanding the Line of Best Fit
The line of best fit is a straight line that best represents the trend in a set of data points. It aims to minimize the overall distance between the line and all the data points. This "best" line is determined using statistical methods, primarily the method of least squares. The equation of the line of best fit is typically represented in the slope-intercept form: y = mx + c, where:
- y is the dependent variable
- x is the independent variable
- m is the slope of the line (representing the rate of change of y with respect to x)
- c is the y-intercept (the value of y when x = 0)
Methods for Calculating the Line of Best Fit
Several methods can calculate the line of best fit. However, the most common and widely used is the method of least squares. This method aims to minimize the sum of the squared vertical distances between each data point and the regression line.
The Method of Least Squares: A Detailed Explanation
The method of least squares involves calculating the slope (m) and y-intercept (c) using the following formulas:
-
m = Σ[(xi - x̄)(yi - ȳ)] / Σ[(xi - x̄)²]
-
c = ȳ - m x̄
Where:
- xi and yi represent the individual data points.
- x̄ is the mean (average) of the x values.
- ȳ is the mean (average) of the y values.
- Σ denotes summation (adding up all the values).
These formulas might look daunting, but they're essentially a systematic way of finding the line that best fits the data. Calculating these manually, especially with a large dataset, is prone to error. This is where a line of best fit equation calculator significantly simplifies the process.
The Power of a Line of Best Fit Equation Calculator
Using a line of best fit equation calculator offers several significant advantages:
-
Accuracy: Calculators minimize human error in calculations, ensuring precise results. Manual calculations, especially with numerous data points, are susceptible to mistakes.
-
Efficiency: Calculators drastically reduce calculation time. What might take hours manually can be done in seconds using a calculator. This is particularly useful when analyzing large datasets or performing multiple regression analyses.
-
Ease of Use: Most online calculators have intuitive interfaces, making them accessible even to users with limited statistical knowledge. Simply input the data points, and the calculator provides the equation of the line of best fit instantly.
-
Visualization: Many calculators provide a visual representation of the data points and the line of best fit, making it easier to understand the relationship between variables and the accuracy of the fit.
-
Advanced Features: Some advanced calculators may offer additional features, such as calculating the correlation coefficient (R), which measures the strength and direction of the linear relationship between the variables. A higher absolute value of R (closer to 1 or -1) indicates a stronger linear correlation. A value of 0 indicates no linear correlation.
Practical Applications of the Line of Best Fit
The line of best fit has numerous applications across various fields:
-
Predictive Modeling: Once the line of best fit is determined, it can be used to predict future values of the dependent variable based on the independent variable. For example, predicting sales based on advertising expenditure or predicting crop yield based on rainfall.
-
Trend Analysis: The line of best fit reveals the overall trend in the data. This is crucial in identifying patterns and making informed decisions. For example, analyzing sales trends over time to understand growth or decline.
-
Data Interpretation: The line of best fit helps to summarize and simplify large datasets, making them easier to interpret and communicate.
-
Scientific Research: In scientific research, the line of best fit is used to model relationships between variables and test hypotheses.
-
Engineering and Technology: Engineers use the line of best fit in designing systems and predicting performance.
-
Finance: Financial analysts employ regression analysis (using the line of best fit) to predict stock prices, interest rates, and other financial variables.
-
Economics: Economists use the line of best fit to model economic relationships and make predictions about macroeconomic variables.
Choosing the Right Line of Best Fit Equation Calculator
When selecting a calculator, consider the following factors:
- Ease of Use: Opt for a calculator with a user-friendly interface.
- Accuracy: Ensure the calculator utilizes reliable algorithms and provides accurate results.
- Features: Consider the additional features offered, such as R-value calculation and data visualization.
- Data Input Methods: Check if the calculator supports different data input methods (manual entry, CSV upload, etc.).
Troubleshooting Common Issues
While using a line of best fit equation calculator is generally straightforward, some common issues might arise:
-
Outliers: Outliers (data points significantly different from the rest) can heavily influence the line of best fit. Consider removing or down-weighting outliers if appropriate.
-
Non-linear Relationships: The method of least squares assumes a linear relationship between variables. If the relationship is non-linear, the line of best fit will not accurately represent the data. Consider using non-linear regression techniques in such cases.
-
Data Errors: Ensure the input data is accurate and free of errors. Even small errors in the data can affect the results.
Conclusion
The line of best fit is a powerful tool for analyzing data and making predictions. While manual calculation is possible, a line of best fit equation calculator is highly recommended for its accuracy, efficiency, and ease of use. By understanding the principles behind the line of best fit and utilizing a reliable calculator, you can effectively analyze your data and draw meaningful insights. Remember to always consider potential issues such as outliers and non-linear relationships for a more accurate and robust analysis. The right calculator empowers you to focus on interpreting results rather than getting bogged down in complex calculations, ultimately allowing for more effective decision-making and data-driven insights. Choosing the right tool significantly improves the overall data analysis workflow, making it efficient and less error-prone.
Latest Posts
Latest Posts
-
What Is One Eighth As A Percentage
Mar 29, 2025
-
Solve X 3 1 7 15
Mar 29, 2025
-
How Much Cerebral Capacity Do Dolphins Use
Mar 29, 2025
-
The Original Three Components Of The Cell Theory Are That
Mar 29, 2025
-
Give The Temperature And Pressure At Stp
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Line Of Best Fit Equation Calculator . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
