Least Common Multiple Of 5 And 12
Juapaving
Apr 01, 2025 · 5 min read
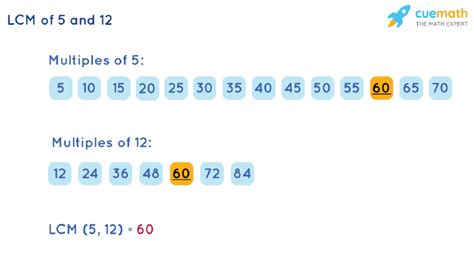
Table of Contents
Unveiling the Least Common Multiple (LCM) of 5 and 12: A Deep Dive
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and exploring different methods to solve it opens doors to a deeper appreciation of number theory and its applications. This comprehensive guide delves into the LCM of 5 and 12, exploring various approaches, highlighting their strengths and weaknesses, and showcasing the practical relevance of LCM calculations in diverse fields.
Understanding the Least Common Multiple (LCM)
Before we delve into the specifics of finding the LCM of 5 and 12, let's establish a firm understanding of what the LCM actually represents. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the given integers. In simpler terms, it's the smallest number that all the given numbers can divide into without leaving a remainder.
This concept is crucial in various mathematical operations and real-world applications, such as:
- Scheduling: Determining when events that occur at regular intervals will coincide again. For instance, if two machines operate on cycles of 5 and 12 hours respectively, finding the LCM helps determine when they'll both be idle simultaneously.
- Fraction arithmetic: Finding a common denominator when adding or subtracting fractions. The LCM of the denominators ensures accurate calculations.
- Modular arithmetic: Solving problems involving congruences and remainders.
- Music theory: Determining the lowest common denominator of musical notes, creating harmonic sequences and chords.
Methods for Calculating the LCM of 5 and 12
Several effective methods exist to calculate the LCM of 5 and 12. Let's explore the most common ones:
1. Listing Multiples Method
This is the most straightforward approach, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60,...
- Multiples of 12: 12, 24, 36, 48, 60,...
By comparing the two lists, we readily identify that the smallest common multiple is 60. This method works well for smaller numbers but becomes cumbersome for larger numbers.
2. Prime Factorization Method
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers. Here's how it works:
-
Find the prime factorization of each number:
- 5 = 5 (5 is a prime number)
- 12 = 2² × 3
-
Identify the highest power of each prime factor: We have 2², 3, and 5.
-
Multiply the highest powers together: LCM(5, 12) = 2² × 3 × 5 = 4 × 3 × 5 = 60
This method is more efficient for larger numbers than the listing method, as it avoids generating extensive lists of multiples. It provides a more structured and systematic approach.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of two numbers are intimately related. They are connected through the following formula:
LCM(a, b) = (|a × b|) / GCD(a, b)
First, we need to find the GCD of 5 and 12. Since 5 is a prime number and 12 is not divisible by 5, the GCD(5, 12) = 1.
Therefore, LCM(5, 12) = (5 × 12) / 1 = 60
This method requires understanding and calculating the GCD, which can be done using various techniques like the Euclidean algorithm. The Euclidean algorithm is particularly efficient for larger numbers.
Applications of LCM(5, 12) in Real-World Scenarios
The LCM of 5 and 12, being 60, finds applications in a surprisingly diverse range of scenarios. Let's explore some practical examples:
1. Gear Ratios: In mechanical engineering, gear ratios often involve finding the LCM to determine when two gears will align again after a certain number of rotations. If one gear has 5 teeth and another has 12 teeth, they will be perfectly aligned again after 60 rotations of the smaller gear (or 25 rotations of the larger gear).
2. Scheduling Tasks: Imagine you need to perform two tasks. Task A takes 5 hours, and task B takes 12 hours. If you start both tasks simultaneously, the next time both tasks will finish at the same time is after 60 hours.
3. Project Management: In large projects, various phases and sub-tasks might have different durations. Understanding the LCM of these durations is crucial for effective scheduling and resource allocation. For example, if two parts of a project require 5 and 12 days respectively, the next time you can simultaneously commence those phases is after 60 days.
4. Music Theory: In music theory, the LCM finds applications in determining when two musical notes with different frequencies will align again to create a harmonious sound or to calculate the shortest period that contains an integer number of both notes.
Extending the Concept: LCM of More Than Two Numbers
The methods discussed above can be extended to find the LCM of more than two numbers. The prime factorization method is particularly adaptable. For instance, let's find the LCM of 5, 12, and 15:
-
Prime Factorization:
- 5 = 5
- 12 = 2² × 3
- 15 = 3 × 5
-
Highest Powers: The highest powers of the prime factors are 2², 3, and 5.
-
Multiplication: LCM(5, 12, 15) = 2² × 3 × 5 = 60
Conclusion: The Significance of LCM Calculations
Understanding and calculating the least common multiple is a fundamental skill in mathematics with far-reaching applications. While the calculation might seem straightforward for small numbers like 5 and 12, mastering the underlying principles and diverse methods allows for efficient problem-solving in more complex scenarios. From scheduling tasks to designing mechanical systems, the LCM plays a critical role in optimizing various processes and ensuring smooth operations. This exploration of the LCM of 5 and 12 has provided a foundation for tackling more challenging LCM problems and appreciating the elegance and practicality of this essential mathematical concept. The diverse methods illustrated, coupled with real-world examples, highlight the versatility and importance of LCM calculations across numerous disciplines.
Latest Posts
Latest Posts
-
Convert 100 Degrees Celsius To Fahrenheit
Apr 02, 2025
-
How To Find Period Of A Trig Eqn
Apr 02, 2025
-
How Tall Is 41 Inches In Feet
Apr 02, 2025
-
Can A Rational Number Be Negative
Apr 02, 2025
-
Unit Of Heat That Measures In The Energy In Food
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 5 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
