Least Common Multiple 7 And 9
Juapaving
Apr 03, 2025 · 5 min read
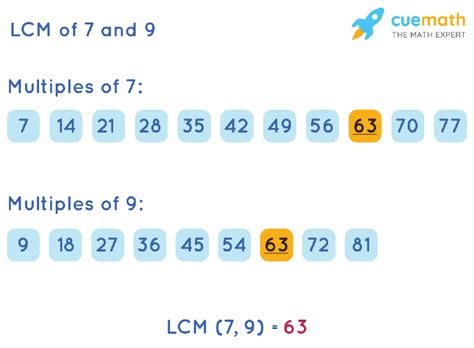
Table of Contents
Finding the Least Common Multiple (LCM) of 7 and 9: A Deep Dive
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding LCMs is crucial for simplifying fractions, solving problems involving ratios and proportions, and even in more advanced mathematical fields. This article will provide a comprehensive exploration of how to find the least common multiple of 7 and 9, covering various methods and their underlying principles. We'll also delve into the broader significance of LCMs in different mathematical contexts.
Understanding Least Common Multiples
Before we tackle the specific case of 7 and 9, let's solidify our understanding of LCMs. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
For instance, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12, and so on. Multiples of 3 are 3, 6, 9, 12, 15, and so on. The common multiples of 2 and 3 are 6, 12, 18, etc. The smallest of these common multiples is 6, therefore, the LCM of 2 and 3 is 6.
Methods for Finding the LCM of 7 and 9
Several methods exist for calculating the LCM, each with its own advantages and disadvantages. Let's examine the most common approaches for determining the LCM of 7 and 9.
1. Listing Multiples Method
This is a straightforward method, especially for smaller numbers. We simply list the multiples of each number until we find the smallest common multiple.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72...
By comparing the lists, we observe that the smallest common multiple is 63. Therefore, the LCM(7, 9) = 63.
This method is simple to understand and visualize, but it can become cumbersome and time-consuming for larger numbers.
2. Prime Factorization Method
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers. This approach is more efficient for larger numbers.
- Prime factorization of 7: 7 (7 is a prime number)
- Prime factorization of 9: 3 x 3 = 3²
To find the LCM using prime factorization:
- Identify all prime factors: The prime factors involved are 3 and 7.
- Take the highest power of each prime factor: The highest power of 3 is 3², and the highest power of 7 is 7¹.
- Multiply the highest powers: LCM(7, 9) = 3² x 7 = 9 x 7 = 63
This method is generally more efficient than listing multiples, especially when dealing with larger numbers or multiple numbers.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of two numbers are related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This relationship can be expressed as:
LCM(a, b) x GCD(a, b) = a x b
To use this method:
- Find the GCD of 7 and 9: Since 7 and 9 have no common factors other than 1, their GCD is 1.
- Apply the formula: LCM(7, 9) x GCD(7, 9) = 7 x 9
- Solve for LCM: LCM(7, 9) = (7 x 9) / GCD(7, 9) = 63 / 1 = 63
This method is particularly useful when the GCD is easily determined, especially using the Euclidean algorithm for larger numbers.
Applications of LCM in Real-World Scenarios
The concept of LCM extends far beyond simple mathematical exercises. It finds practical applications in various real-world situations:
-
Scheduling: Imagine two buses leave a terminal at different intervals. One leaves every 7 minutes, and the other every 9 minutes. The LCM helps determine when both buses will depart simultaneously again (after 63 minutes). This is crucial for efficient scheduling in transportation and other logistical operations.
-
Fractions and Arithmetic: Finding a common denominator when adding or subtracting fractions involves calculating the LCM of the denominators. This ensures accurate calculations and simplifies the process.
-
Patterning and Cycles: LCM is useful in identifying repeating patterns or cycles. For example, in repeating decimal expansions, the length of the repeating block is often related to the LCM of certain numbers.
-
Engineering and Construction: The LCM is used in various engineering applications, such as determining the optimal timing of synchronized machinery or the least common length for cutting materials to avoid waste.
-
Music Theory: LCM plays a role in music theory, particularly in determining harmonic intervals and the least common period for rhythmic patterns.
LCM and Relatively Prime Numbers
Two numbers are considered relatively prime (or coprime) if their greatest common divisor (GCD) is 1. In the case of 7 and 9, since their GCD is 1, they are relatively prime. A notable property of relatively prime numbers is that their LCM is simply their product. This simplifies the calculation significantly.
This means that for relatively prime numbers a and b:
LCM(a, b) = a x b
Expanding the Concept: LCM of More Than Two Numbers
The methods discussed above can be extended to find the LCM of more than two numbers. The prime factorization method is particularly efficient in this case. For example, to find the LCM of 7, 9, and 5:
-
Prime factorization:
- 7 = 7
- 9 = 3²
- 5 = 5
-
Highest powers: The highest powers of the prime factors are 3², 5¹, and 7¹.
-
Multiply: LCM(7, 9, 5) = 3² x 5 x 7 = 9 x 5 x 7 = 315
Conclusion: The Significance of LCM
The least common multiple is a fundamental concept with broad applications across numerous fields. Mastering the different methods for calculating the LCM, particularly the prime factorization method, equips you with a powerful tool for problem-solving in mathematics and beyond. Understanding the relationship between LCM and GCD further enhances your mathematical proficiency. Whether you're dealing with simple arithmetic or more complex scenarios, the LCM remains a crucial element in understanding numerical relationships and patterns. The example of finding the LCM of 7 and 9, while seemingly straightforward, provides a solid foundation for grasping the broader implications of this vital mathematical concept.
Latest Posts
Latest Posts
-
Are Humans Warm Blooded Or Cold Blooded
Apr 03, 2025
-
What Is 0 08 As A Percent
Apr 03, 2025
-
How Many Chambers Does A Fish Heart Have
Apr 03, 2025
-
How Many 3 Digit Numbers Are There
Apr 03, 2025
-
An Organism That Can Make Its Own Food
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple 7 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
