Equation Of Circle In Parametric Form
Juapaving
Apr 02, 2025 · 5 min read
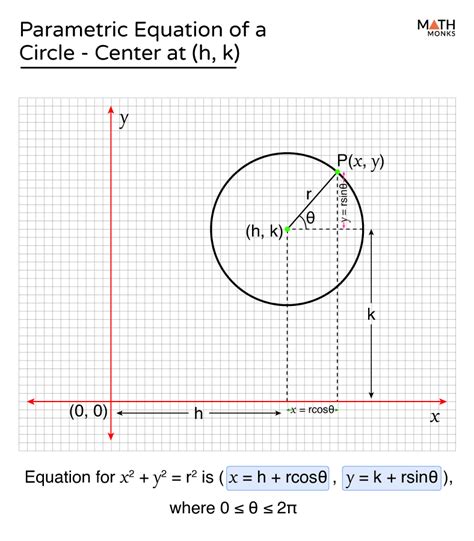
Table of Contents
The Equation of a Circle in Parametric Form: A Comprehensive Guide
The equation of a circle in its standard form, (x - h)² + (y - k)² = r², provides a concise description of the circle's properties: center (h, k) and radius r. However, this Cartesian representation doesn't explicitly describe the points on the circle as a function of a single parameter. This is where the parametric form shines, offering a dynamic and versatile way to represent a circle. This article delves deep into the parametric equation of a circle, exploring its derivation, various forms, applications, and its advantages over the standard form.
Understanding Parametric Equations
Before diving into the circle's parametric form, let's briefly review the concept of parametric equations. A parametric equation represents a set of quantities as functions of one or more independent variables, called parameters. Instead of directly relating x and y, as in the standard Cartesian equation, parametric equations express both x and y in terms of a third variable, often denoted as 't'. This parameter, 't', can be thought of as a time variable, an angle, or any other independent variable.
For instance, a simple parametric equation could be:
- x = t
- y = t²
These equations define a parabola. As 't' varies, the coordinates (x, y) trace out the shape of the parabola.
Deriving the Parametric Equation of a Circle
The most common parametric representation of a circle utilizes trigonometric functions, sine and cosine. Consider a circle centered at the origin (0, 0) with radius 'r'. Any point (x, y) on this circle can be defined using the angle θ (theta) it makes with the positive x-axis. From basic trigonometry:
- x = r * cos(θ)
- y = r * sin(θ)
where:
- r represents the radius of the circle.
- θ (theta) is the angle between the positive x-axis and the line segment connecting the origin to the point (x, y) on the circle. θ varies from 0 to 2π radians (or 0 to 360 degrees) to cover the entire circle.
These two equations form the fundamental parametric representation of a circle centered at the origin. As θ increases from 0 to 2π, the point (x, y) traces out the entire circle in a counter-clockwise direction.
Shifting the Center: Parametric Equation of a Circle with Center (h, k)
To generalize the parametric equation for a circle not centered at the origin, we simply translate the coordinates. If the center is at (h, k), the parametric equations become:
- x = h + r * cos(θ)
- y = k + r * sin(θ)
This shifts the entire circle so that its center lies at (h, k) while maintaining the radius 'r'. Again, θ ranges from 0 to 2π radians.
Different Parameterizations: Exploring Alternative Forms
While the trigonometric form (using sine and cosine) is the most common and intuitive, other parameterizations exist. These alternative forms can be useful in specific contexts or might offer computational advantages.
One such alternative uses the parameter 't' directly:
- x = r * (1 - t²) / (1 + t²)
- y = 2rt / (1 + t²)
This form, derived from the rational parameterization of a circle, avoids the use of trigonometric functions. It's important to note that this parameterization doesn't cover the entire circle for a single pass of 't'. It typically requires the interval for 't' to be (-∞, ∞) to cover all the points on the circle.
Another interesting approach employs hyperbolic functions:
- x = r * cosh(t)
- y = r * sinh(t)
This parameterization, however, generates only one half of the circle. It's useful in certain mathematical contexts, but less common for general circle representations.
Applications of the Parametric Equation of a Circle
The parametric form of a circle is not merely a theoretical curiosity; it finds widespread applications in various fields:
-
Computer Graphics: In computer graphics and animation, parametric equations are essential for creating smooth and efficient representations of circles and circular arcs. They allow for easy control over the shape and movement of objects along circular paths.
-
Robotics: In robotics and automation, parametric equations are used to define the trajectory of robotic arms and other moving parts. Circular movements are common in robotic applications, and parametric equations provide a clean and efficient way to describe them.
-
Physics and Engineering: Many physical phenomena involve circular motion. Parametric equations provide a powerful tool to model and analyze these motions. Examples include planetary orbits, rotating machinery, and wave propagation.
-
Calculus and Differential Geometry: The parametric form facilitates the study of tangent lines, curvature, and other geometric properties of the circle more easily than the Cartesian form, especially when considering rates of change along the curve.
-
Game Development: In game development, parametric equations are used to control the movement of objects along circular paths, create realistic animations, and generate various game elements.
Advantages of Parametric Form over Standard Form
The parametric form offers several advantages over the standard Cartesian equation of a circle:
-
Flexibility and Control: Parametric equations offer greater flexibility in controlling the trajectory and speed of a point moving along the circle. This is particularly beneficial in animation and simulations.
-
Ease of Differentiation and Integration: In calculus, parametric equations simplify the computation of derivatives and integrals. Finding the tangent to a circle at a given point or calculating the arc length becomes more straightforward using the parametric representation.
-
Direct Representation of Motion: The parameter 't' can be intuitively interpreted as time, offering a clear representation of the motion of a point along the circle.
-
Handling of Partial Circles (Arcs): It's easy to define only a portion of a circle by restricting the range of the parameter 'θ'. For example, to represent a semicircle, we'd constrain θ from 0 to π.
Conclusion
The parametric equation of a circle, specifically utilizing trigonometric functions, provides a robust and versatile method to represent circles in various contexts. Its advantages over the standard Cartesian form, particularly in areas such as animation, robotics, and calculus, make it an indispensable tool in many disciplines. Understanding the derivation, different forms, and applications of the parametric equation of a circle empowers professionals and students alike to model and manipulate circular shapes with greater precision and efficiency. While the trigonometric form is widely used and readily understood, appreciating the existence of alternative parameterizations broadens the toolkit for tackling more complex problems. Remember to choose the parameterization that best suits your specific application and computational needs.
Latest Posts
Latest Posts
-
Biotic Factors In An Aquatic Ecosystem
Apr 03, 2025
-
Least Common Multiple Of 10 And 8
Apr 03, 2025
-
Four Ways To Write A Number
Apr 03, 2025
-
How To Calculate The Perimeter Of A Rhombus
Apr 03, 2025
-
Is The Electromagnetic Spectrum Transverse Or Longitudinal
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Equation Of Circle In Parametric Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
