Least Common Multiple 12 And 16
Juapaving
Apr 01, 2025 · 5 min read
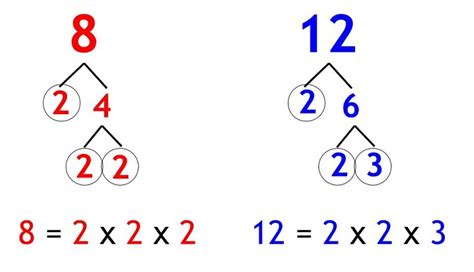
Table of Contents
Finding the Least Common Multiple (LCM) of 12 and 16: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and algebra. Understanding LCMs is crucial for various applications, from simplifying fractions to solving problems involving periodic events. This article delves deep into the calculation and significance of the least common multiple of 12 and 16, exploring different methods and highlighting practical examples. We'll also touch upon the broader context of LCMs and their applications beyond simple arithmetic.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all of the integers. In simpler terms, it's the smallest number that contains all the numbers as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3.
Methods for Finding the LCM of 12 and 16
Several methods can be employed to determine the LCM of 12 and 16. Let's explore the most common approaches:
1. Listing Multiples Method
This straightforward method involves listing the multiples of each number until a common multiple is found. The smallest common multiple is the LCM.
- Multiples of 12: 12, 24, 36, 48, 60, 72, 96, 108, 120...
- Multiples of 16: 16, 32, 48, 64, 80, 96, 112, 128...
Notice that 48 and 96 appear in both lists. However, 48 is the smallest common multiple; therefore, the LCM of 12 and 16 is 48. While effective for smaller numbers, this method becomes less efficient as the numbers increase in size.
2. Prime Factorization Method
This method utilizes the prime factorization of each number. The prime factorization is the expression of a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
- Prime factorization of 16: 2 x 2 x 2 x 2 = 2⁴
To find the LCM using prime factorization:
- Identify all the prime factors: In this case, the prime factor is 2 and 3.
- Take the highest power of each prime factor: The highest power of 2 is 2⁴ (from the factorization of 16), and the highest power of 3 is 3¹ (from the factorization of 12).
- Multiply the highest powers together: 2⁴ x 3¹ = 16 x 3 = 48.
Therefore, the LCM of 12 and 16 is 48. This method is generally more efficient than listing multiples, especially when dealing with larger numbers.
3. Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest positive integer that divides both numbers without leaving a remainder. The relationship between LCM and GCD is given by the formula:
LCM(a, b) x GCD(a, b) = a x b
where 'a' and 'b' are the two numbers.
- Find the GCD of 12 and 16: The divisors of 12 are 1, 2, 3, 4, 6, and 12. The divisors of 16 are 1, 2, 4, 8, and 16. The greatest common divisor is 4.
- Apply the formula: LCM(12, 16) x GCD(12, 16) = 12 x 16 LCM(12, 16) x 4 = 192 LCM(12, 16) = 192 / 4 = 48
This method is particularly useful when dealing with larger numbers where finding the prime factorization might be more challenging. Finding the GCD can be done using the Euclidean algorithm, which is an efficient method for finding the GCD of two numbers.
Applications of LCM
The LCM finds applications in diverse areas:
-
Fraction Addition and Subtraction: When adding or subtracting fractions with different denominators, finding the LCM of the denominators allows you to rewrite the fractions with a common denominator, facilitating the calculation.
-
Scheduling Problems: The LCM is useful in solving problems related to repeating events. For example, if two buses arrive at a stop every 12 minutes and 16 minutes respectively, the LCM (48 minutes) determines when they will arrive simultaneously.
-
Music Theory: The LCM is applied in determining the least common multiple of different musical rhythms, helping to synchronize musical parts within a composition.
-
Gear Ratios: In mechanics, the LCM is useful in determining the least common multiple of different gear ratios in a gear train. This is vital in calculating the speed and torque output of a gear train.
-
Computer Science: LCM is used in various algorithms and data structures. In scheduling processes in an operating system, LCM can help in optimizing the execution of tasks.
-
Pattern Recognition: In various fields, the LCM can help identify the repetition of events or cycles within datasets, useful in various kinds of data analysis.
LCM in Real-World Scenarios
Let's consider some real-world examples where understanding the LCM is crucial:
Scenario 1: Concert Scheduling: Two bands are scheduled to perform at a music festival. Band A plays every 12 minutes, and Band B plays every 16 minutes. How long will it take until both bands play simultaneously?
The LCM of 12 and 16 (48 minutes) determines that both bands will play together after 48 minutes.
Scenario 2: Traffic Light Synchronization: Two traffic lights on a busy street cycle every 12 seconds and 16 seconds, respectively. When will they both turn green simultaneously?
The LCM of 12 and 16 is 48 seconds. Both traffic lights will turn green at the same time every 48 seconds.
Scenario 3: Manufacturing Process: Two machines in a factory produce parts at different rates. Machine A produces a part every 12 minutes, while Machine B produces a part every 16 minutes. At what time interval will both machines produce a part simultaneously?
The LCM of 12 and 16 (48 minutes) indicates that both machines will produce a part at the same time every 48 minutes.
Conclusion
The least common multiple (LCM) is a fundamental concept with practical applications across various fields. Understanding the different methods for calculating the LCM, such as the listing multiples method, prime factorization method, and GCD method, allows one to efficiently determine the LCM of any two or more integers. The examples presented demonstrate the real-world significance of the LCM, highlighting its usefulness in solving problems related to scheduling, synchronization, and various other applications in manufacturing and more. Proficiency in calculating LCMs is a valuable skill for anyone working with numbers and problem-solving across various domains. The concept of LCM extends beyond simple arithmetic and is a fundamental building block in more advanced mathematical concepts.
Latest Posts
Latest Posts
-
What Is The Lowest Common Multiple Of 3 And 7
Apr 02, 2025
-
How To Find A Supplementary Angle
Apr 02, 2025
-
How Can The Strength Of An Electromagnet Be Increased
Apr 02, 2025
-
If Qt Is Perpendicular To Pr
Apr 02, 2025
-
Which Base Is Not Present In Rna
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple 12 And 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
