Lcm Of 9 6 And 3
Juapaving
May 09, 2025 · 5 min read
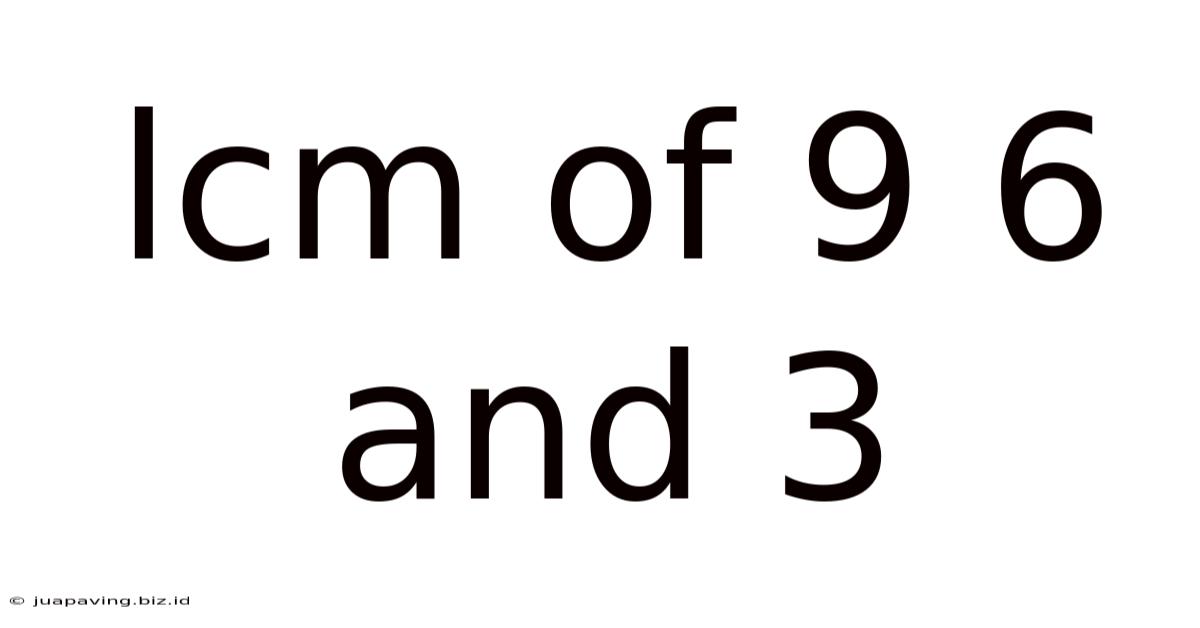
Table of Contents
Finding the Least Common Multiple (LCM) of 9, 6, and 3: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and algebra. Understanding how to calculate the LCM is crucial for various applications, from simplifying fractions to solving problems in fields like physics and computer science. This comprehensive guide will delve into the process of finding the LCM of 9, 6, and 3, exploring different methods and providing a solid understanding of the underlying principles. We'll also examine the broader context of LCMs and their significance in mathematical operations.
Understanding Least Common Multiples (LCMs)
Before we dive into calculating the LCM of 9, 6, and 3, let's establish a clear understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that contains all the given numbers as factors.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12... Multiples of 3 are 3, 6, 9, 12, 15... The common multiples of 2 and 3 are 6, 12, 18... The smallest of these common multiples is 6, so the LCM(2, 3) = 6.
Methods for Calculating the LCM
Several methods exist for calculating the LCM of a set of numbers. We'll explore the most common and effective approaches, focusing on their application to finding the LCM of 9, 6, and 3.
1. Listing Multiples Method
This is a straightforward method, especially suitable for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 9: 9, 18, 27, 36, 45, 54...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 36...
By inspecting the lists, we observe that the smallest common multiple of 9, 6, and 3 is 18. Therefore, LCM(9, 6, 3) = 18. This method is simple but can become cumbersome for larger numbers.
2. Prime Factorization Method
This is a more efficient method, particularly useful for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the highest powers of each prime factor present.
- Prime factorization of 9: 3²
- Prime factorization of 6: 2 × 3
- Prime factorization of 3: 3
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2¹ (from 6).
- The highest power of 3 is 3² (from 9).
Therefore, LCM(9, 6, 3) = 2¹ × 3² = 2 × 9 = 18.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of a set of numbers are related. The product of the LCM and GCD of two numbers is equal to the product of the numbers themselves. While this method is less intuitive for multiple numbers, it can be adapted. We'll first find the GCD of 9, 6, and 3 using the Euclidean algorithm, and then leverage the relationship to find the LCM.
-
Finding the GCD of 9, 6, and 3:
- GCD(9, 6) = 3 (using the Euclidean algorithm: 9 = 1 × 6 + 3; 6 = 2 × 3 + 0)
- GCD(3, 3) = 3
-
Using the relationship between LCM and GCD: This relationship doesn't directly extend to three or more numbers in a simple formula. However, we can use the prime factorization method in conjunction with this understanding. Since we know the GCD(9,6,3) = 3, and we know the prime factors, this helps to simplify the prime factorization method.
Applications of LCMs
The concept of LCM finds extensive applications in various mathematical and real-world scenarios:
-
Fraction Addition and Subtraction: Finding the LCM of the denominators is essential when adding or subtracting fractions with different denominators. This ensures that we have a common denominator for the operation.
-
Scheduling Problems: LCMs are used in scheduling problems, such as determining when events that occur at regular intervals will coincide. For example, if two machines operate on cycles of 9 and 6 hours, respectively, the LCM will tell you when they will both be at the starting point of their cycles simultaneously.
-
Modular Arithmetic: LCMs play a crucial role in modular arithmetic, which is used in cryptography and other areas of computer science.
-
Music Theory: The concept of LCM helps determine the least common period of rhythmic patterns.
-
Engineering: LCMs are useful in scenarios involving synchronized events or processes.
Expanding on the LCM of 9, 6, and 3
Let's further explore the implications of the LCM(9, 6, 3) = 18. This signifies that 18 is the smallest number that is evenly divisible by 9, 6, and 3. This simple result has significant implications in various mathematical contexts. For example, if you were working with fractions having denominators of 9, 6, and 3, you would find the common denominator to be 18. This allows for the seamless addition and subtraction of these fractions.
Beyond the Basics: LCMs and More Complex Scenarios
While we've focused on finding the LCM of three relatively small numbers, the principles extend to larger sets of numbers and more complex scenarios. For instance, calculating the LCM of many numbers efficiently requires employing the prime factorization method. For larger numbers, the prime factorization might necessitate sophisticated algorithms.
Conclusion
Finding the least common multiple is a fundamental skill with far-reaching applications. Mastering various methods, such as the listing multiples, prime factorization, and GCD-based approaches, provides a versatile toolkit for solving a wide range of mathematical problems. Understanding the underlying principles and applications of LCMs is crucial for anyone pursuing further studies in mathematics, computer science, or related fields. The seemingly simple task of finding the LCM(9, 6, 3) = 18 serves as a gateway to understanding a much broader and essential mathematical concept. By grasping the principles outlined in this guide, you will develop a robust foundation for tackling more complex LCM problems and various real-world applications.
Latest Posts
Latest Posts
-
What Is The Difference Between A Prism And Pyramid
May 11, 2025
-
Subject Verb Agreement Worksheet Class 7
May 11, 2025
-
Which Is A Limitation Of Scientific Management
May 11, 2025
-
Words That Start And End With V
May 11, 2025
-
What Is Lcm Of 7 And 12
May 11, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 9 6 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.