Lcm Of 8 10 And 12
Juapaving
Mar 25, 2025 · 5 min read
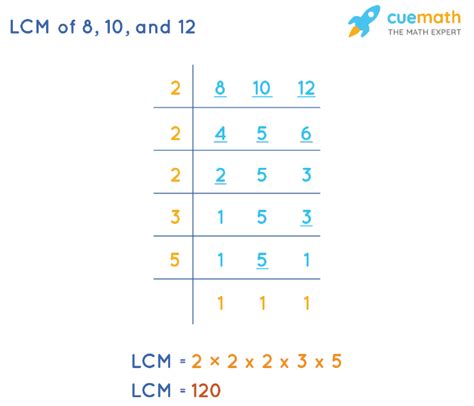
Table of Contents
Finding the LCM of 8, 10, and 12: A Comprehensive Guide
Determining the Least Common Multiple (LCM) of numbers is a fundamental concept in mathematics with wide-ranging applications, from simplifying fractions to solving complex scheduling problems. This comprehensive guide delves into the process of finding the LCM of 8, 10, and 12, exploring various methods and offering a deeper understanding of the underlying principles. We'll cover different approaches, including prime factorization, listing multiples, and using the greatest common divisor (GCD). By the end, you'll be equipped to tackle LCM problems with confidence.
Understanding Least Common Multiple (LCM)
Before diving into the calculation, let's solidify our understanding of the LCM. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
For instance, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12... and the multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Method 1: Prime Factorization
This method is generally considered the most efficient and systematic way to find the LCM of larger numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Step 1: Prime Factorization of Each Number
Let's find the prime factorization of 8, 10, and 12:
- 8: 2 x 2 x 2 = 2³
- 10: 2 x 5
- 12: 2 x 2 x 3 = 2² x 3
Step 2: Identify the Highest Power of Each Prime Factor
Looking at the prime factorizations, we identify the highest power of each prime factor present:
- The highest power of 2 is 2³ (from the factorization of 8).
- The highest power of 3 is 3¹ (from the factorization of 12).
- The highest power of 5 is 5¹ (from the factorization of 10).
Step 3: Multiply the Highest Powers Together
To find the LCM, we multiply these highest powers together:
LCM(8, 10, 12) = 2³ x 3 x 5 = 8 x 3 x 5 = 120
Therefore, the LCM of 8, 10, and 12 is 120.
Method 2: Listing Multiples
This method is suitable for smaller numbers but becomes less efficient as the numbers get larger. It involves listing the multiples of each number until a common multiple is found.
Step 1: List Multiples of Each Number
Let's list the multiples of 8, 10, and 12:
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130...
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132...
Step 2: Identify the Smallest Common Multiple
The smallest number that appears in all three lists is 120.
Therefore, the LCM of 8, 10, and 12 is 120.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) are closely related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
This formula can be extended to more than two numbers, but it becomes more complex. We can use this relationship to find the LCM if we first find the GCD.
Step 1: Find the GCD of 8, 10, and 12
The GCD is the largest number that divides all three numbers without leaving a remainder. We can find this using the prime factorization method:
- 8: 2³
- 10: 2 x 5
- 12: 2² x 3
The only common prime factor is 2, and the lowest power is 2¹. Therefore, GCD(8, 10, 12) = 2.
Step 2: Apply the LCM/GCD Formula (Extension Required)
The formula LCM(a, b) x GCD(a, b) = a x b doesn't directly extend to three numbers in a simple way. While we can find the LCM of two numbers using this method and then find the LCM of that result with the third number, it's less efficient than the prime factorization method for multiple numbers. For this reason, the prime factorization method is generally preferred for finding the LCM of three or more numbers.
Applications of LCM
The concept of LCM has practical applications across various fields:
Scheduling Problems:
Imagine you have three tasks that repeat at different intervals. Task A repeats every 8 days, Task B every 10 days, and Task C every 12 days. To find when all three tasks will coincide, you need to find the LCM of 8, 10, and 12, which is 120. This means all three tasks will occur simultaneously every 120 days.
Fraction Arithmetic:
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial for finding a common denominator. This simplifies the addition or subtraction process.
Gear Ratios and Mechanical Systems:
In mechanical engineering, LCM is used to determine the synchronization of gears and other rotating components in systems where components rotate at different speeds.
Music Theory:
LCM plays a role in understanding musical harmony and finding the least common multiple of the frequencies of different notes to determine when they will harmoniously coincide.
Modular Arithmetic and Cryptography:
In advanced mathematics, LCM has applications in modular arithmetic and cryptography.
Conclusion
Finding the least common multiple (LCM) is a vital mathematical skill with a broad spectrum of practical applications. While various methods exist, the prime factorization method offers the most efficient and systematic approach, especially when dealing with larger numbers or multiple numbers simultaneously. Understanding the LCM not only enhances mathematical proficiency but also provides valuable tools for solving real-world problems in diverse fields. Mastering this concept opens doors to a deeper understanding of mathematical relationships and their impact on our daily lives. The ability to swiftly and accurately calculate the LCM, as demonstrated through the example of finding the LCM of 8, 10, and 12, is an essential skill for anyone working with numbers and problem-solving.
Latest Posts
Latest Posts
-
Is Melting Point An Intensive Or Extensive Property
Mar 29, 2025
-
From Where Do Plants Get Carbon Dioxide
Mar 29, 2025
-
Is 60 A Prime Or Composite Number
Mar 29, 2025
-
Label The Diagram Of The Respiratory System
Mar 29, 2025
-
A Community And Its Abiotic Environment
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 8 10 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
