Lcm Of 6 8 And 12
Juapaving
Mar 26, 2025 · 5 min read
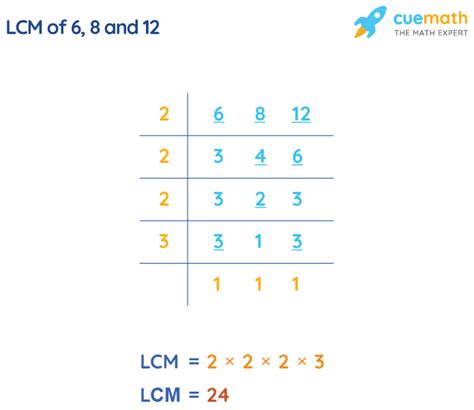
Table of Contents
Finding the LCM of 6, 8, and 12: A Comprehensive Guide
Finding the least common multiple (LCM) of numbers is a fundamental concept in mathematics with wide-ranging applications. This comprehensive guide will delve deep into calculating the LCM of 6, 8, and 12, exploring various methods and highlighting the underlying principles. We'll go beyond the simple calculation and uncover the practical significance of LCM in diverse fields.
Understanding Least Common Multiple (LCM)
Before jumping into the calculation, let's solidify our understanding of LCM. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the given numbers as factors.
For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer that is divisible by both 2 and 3.
Methods for Finding the LCM of 6, 8, and 12
Several effective methods exist for calculating the LCM of numbers. We will explore three common approaches: the listing method, the prime factorization method, and the greatest common divisor (GCD) method.
1. Listing Multiples Method
This method involves listing the multiples of each number until we find the smallest common multiple. Let's apply this to our numbers: 6, 8, and 12.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 72...
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80...
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84...
By comparing the lists, we observe that the smallest common multiple is 24. Therefore, the LCM of 6, 8, and 12 using the listing method is 24. This method is straightforward for smaller numbers but becomes less efficient as the numbers increase in size.
2. Prime Factorization Method
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers. The steps are:
-
Find the prime factorization of each number:
- 6 = 2 × 3
- 8 = 2 × 2 × 2 = 2³
- 12 = 2 × 2 × 3 = 2² × 3
-
Identify the highest power of each prime factor:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
-
Multiply the highest powers together:
- LCM(6, 8, 12) = 2³ × 3 = 8 × 3 = 24
The prime factorization method is generally more efficient than the listing method, especially for larger numbers. It provides a systematic approach to finding the LCM.
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between LCM and GCD. The LCM and GCD of two numbers are related by the following formula:
LCM(a, b) = (|a × b|) / GCD(a, b)
This can be extended to more than two numbers. However, the calculation becomes more complex. Let's first find the GCD of 6, 8, and 12 using the Euclidean algorithm:
-
Find the GCD of 6 and 8:
- 8 = 1 × 6 + 2
- 6 = 3 × 2 + 0
- GCD(6, 8) = 2
-
Find the GCD of the result (2) and 12:
- 12 = 6 × 2 + 0
- GCD(2, 12) = 2
Therefore, the GCD of 6, 8, and 12 is 2. Now we can use this to calculate the LCM: This method is less straightforward for multiple numbers, and we would instead use the prime factorization method or the listing method as illustrated above. However, it's useful to understand the relationship between GCD and LCM.
To find the LCM of 6, 8, and 12 using this relationship would be computationally cumbersome and inefficient in this particular instance. The prime factorization method is far more practical.
Applications of LCM
The concept of LCM extends far beyond simple mathematical exercises. It finds practical applications in various fields:
1. Scheduling and Timing
Imagine you have three machines that perform different tasks in a factory. Machine A completes its cycle every 6 hours, Machine B every 8 hours, and Machine C every 12 hours. To determine when all three machines will complete their cycles simultaneously, we need to find the LCM of 6, 8, and 12. The LCM, 24, indicates that all three machines will complete their cycles simultaneously after 24 hours.
2. Fraction Arithmetic
Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators. For example, to add 1/6 + 1/8 + 1/12, we need to find the LCM of 6, 8, and 12 (which is 24). We then convert each fraction to an equivalent fraction with a denominator of 24 before performing the addition.
3. Music Theory
Musical intervals and rhythms often involve LCM calculations. For example, determining the length of a musical phrase that contains repeating patterns of different lengths involves finding the LCM of those lengths.
4. Engineering and Design
LCM calculations are used in engineering and design to synchronize components that operate at different frequencies or speeds.
5. Modular Arithmetic and Cryptography
In modular arithmetic, which is the basis of many cryptographic systems, the LCM plays a vital role in solving congruences and other related problems.
Conclusion: Mastering LCM Calculations
Understanding and calculating the least common multiple is a critical skill in mathematics with far-reaching applications. We've explored three different methods—listing multiples, prime factorization, and the GCD method—for calculating the LCM of 6, 8, and 12, which is 24. The prime factorization method stands out as the most efficient and reliable approach, especially when dealing with larger numbers. By understanding the various methods and appreciating the widespread applicability of LCM, you'll gain a more profound understanding of its importance in both theoretical mathematics and practical applications across diverse fields. Remember, the key is to choose the most efficient method based on the numbers involved and your comfort level with different mathematical techniques. Mastering LCM is a stepping stone to more advanced mathematical concepts and problem-solving.
Latest Posts
Latest Posts
-
Difference Between Bony Fish And Cartilaginous Fish
Mar 28, 2025
-
The Scattering Of Light By Colloidal Particles
Mar 28, 2025
-
Human Body Temperature In Kelvin Scale
Mar 28, 2025
-
What Is Only Even Prime Number
Mar 28, 2025
-
Vapor Pressure Of Water At 23c
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 6 8 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
