Lcm Of 3 4 And 9
Juapaving
Mar 31, 2025 · 5 min read
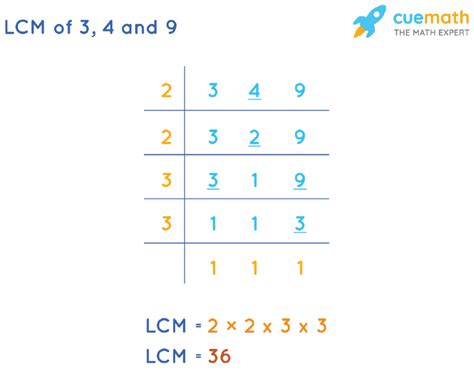
Table of Contents
Finding the Least Common Multiple (LCM) of 3, 4, and 9: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics with wide-ranging applications, from simplifying fractions to solving complex scheduling problems. This article delves into the process of finding the LCM of 3, 4, and 9, providing multiple methods to achieve this, and exploring the underlying mathematical principles. We'll also discuss practical applications and extend the concept to finding the LCM of larger sets of numbers.
Understanding Least Common Multiples
Before we dive into calculating the LCM of 3, 4, and 9, let's establish a solid understanding of the concept. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that contains all the given numbers as factors.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12, ... and the multiples of 3 are 3, 6, 9, 12, 15, ... The smallest number that appears in both lists is 6, therefore, the LCM of 2 and 3 is 6.
Methods for Finding the LCM of 3, 4, and 9
There are several efficient methods for determining the LCM of a set of numbers. Let's explore three common approaches, applying them to find the LCM of 3, 4, and 9:
1. Listing Multiples Method
This method involves listing the multiples of each number until a common multiple is found. While straightforward for smaller numbers, it can become cumbersome with larger numbers.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 36...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36...
- Multiples of 9: 9, 18, 27, 36...
By comparing the lists, we observe that the smallest common multiple is 36. Therefore, the LCM(3, 4, 9) = 36.
2. Prime Factorization Method
This method utilizes the prime factorization of each number. It's a more efficient and systematic approach, especially when dealing with larger numbers.
- Prime factorization of 3: 3 = 3¹
- Prime factorization of 4: 4 = 2²
- Prime factorization of 9: 9 = 3²
To find the LCM, we identify the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3² = 9
Multiply these highest powers together: 2² * 3² = 4 * 9 = 36. Therefore, LCM(3, 4, 9) = 36.
3. Greatest Common Divisor (GCD) Method
This method leverages the relationship between the LCM and the greatest common divisor (GCD) of two or more numbers. The formula connecting LCM and GCD is:
LCM(a, b) * GCD(a, b) = a * b
This can be extended to more than two numbers, but it becomes more complex. For our example, let's initially find the LCM of 3 and 4, and then find the LCM of that result and 9.
- GCD(3, 4) = 1 (3 and 4 share no common factors other than 1)
- LCM(3, 4) = (3 * 4) / GCD(3, 4) = 12 / 1 = 12
- GCD(12, 9) = 3
- LCM(12, 9) = (12 * 9) / GCD(12, 9) = 108 / 3 = 36
Therefore, LCM(3, 4, 9) = 36. This method is particularly useful when dealing with larger numbers where prime factorization might be more tedious.
Applications of LCM
The LCM finds applications in various fields:
-
Fractions: Finding the LCM of the denominators is crucial when adding or subtracting fractions. It allows us to find a common denominator, simplifying the calculation.
-
Scheduling: Determining when events will occur simultaneously. For example, if one event repeats every 3 days, another every 4 days, and a third every 9 days, the LCM will tell us when all three events will coincide.
-
Cyclic Patterns: Identifying when repeating patterns will align. This is useful in various fields, from engineering to music.
-
Modular Arithmetic: The LCM plays a vital role in solving problems involving modular arithmetic, a system of arithmetic for integers.
Extending the Concept: LCM of Larger Sets of Numbers
The methods described above can be readily extended to find the LCM of larger sets of numbers. The prime factorization method remains the most efficient approach for larger sets. For example, to find the LCM of 3, 4, 9, and 6:
-
Prime factorize each number:
- 3 = 3¹
- 4 = 2²
- 9 = 3²
- 6 = 2¹ * 3¹
-
Identify the highest power of each prime factor:
- Highest power of 2: 2² = 4
- Highest power of 3: 3² = 9
-
Multiply the highest powers together: 4 * 9 = 36. Therefore, LCM(3, 4, 9, 6) = 36.
Conclusion: Mastering LCM Calculations
Finding the least common multiple is a fundamental skill with practical applications across numerous mathematical and real-world scenarios. Understanding the different methods—listing multiples, prime factorization, and the GCD method—provides flexibility in approaching LCM problems. While the listing method is intuitive for smaller numbers, the prime factorization method proves highly efficient for larger numbers and larger sets of numbers. Mastering these techniques empowers you to confidently solve a wide range of problems involving LCM calculations. Remember to choose the method that best suits the specific numbers involved for optimal efficiency and accuracy. The consistent practice of these methods will build your mathematical proficiency and problem-solving skills. By understanding the underlying principles and employing the appropriate techniques, you can confidently tackle any LCM problem that comes your way.
Latest Posts
Latest Posts
-
A Letter Or Symbol That Represents A Missing Value
Apr 02, 2025
-
A Slender Homogeneous Rod Of Length 2l
Apr 02, 2025
-
Cervical Thoracic And Lumbar Vertebrae Differences
Apr 02, 2025
-
Are All Cells The Same Shape And Size
Apr 02, 2025
-
What Are Rows Called In The Periodic Table
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 4 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
