Lcm Of 2 5 And 7
Juapaving
Mar 16, 2025 · 5 min read
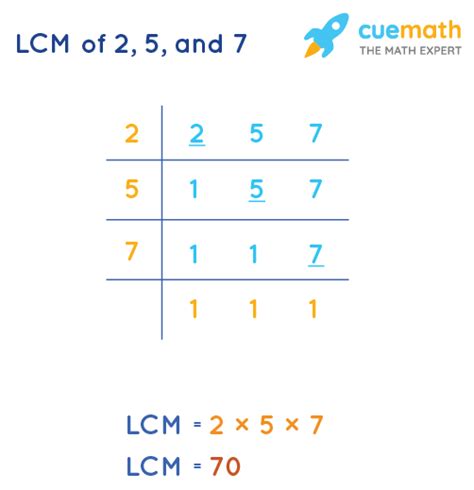
Table of Contents
Finding the LCM of 2, 5, and 7: A Comprehensive Guide
Finding the least common multiple (LCM) of numbers is a fundamental concept in mathematics with applications spanning various fields, from scheduling tasks to simplifying fractions. This article will delve deep into the process of finding the LCM of 2, 5, and 7, exploring different methods and providing a solid understanding of the underlying principles. We'll also touch upon the broader applications of LCM calculations and related concepts.
Understanding Least Common Multiple (LCM)
Before we tackle the specific problem of finding the LCM of 2, 5, and 7, let's define what the LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12... Multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Methods for Calculating LCM
There are several effective methods for calculating the LCM of a set of numbers. Let's explore the most common ones, and then apply them to our specific example of 2, 5, and 7.
1. Listing Multiples Method
This is a straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70...
By examining the lists, we can see that the smallest number common to all three lists is 70. Therefore, the LCM of 2, 5, and 7 is 70. This method works well for small numbers but can become cumbersome for larger numbers.
2. Prime Factorization Method
This is a more efficient method, particularly for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the highest powers of each prime factor present.
- Prime factorization of 2: 2¹
- Prime factorization of 5: 5¹
- Prime factorization of 7: 7¹
Since 2, 5, and 7 are all prime numbers, their prime factorizations are simply themselves raised to the power of 1. To find the LCM, we take the highest power of each prime factor present:
LCM(2, 5, 7) = 2¹ * 5¹ * 7¹ = 70
This method is generally more efficient than listing multiples, especially when dealing with larger numbers or a greater number of integers.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) are closely related. There's a formula that connects them:
LCM(a, b) * GCD(a, b) = a * b
This can be extended to more than two numbers, but the calculation becomes more complex. For 2, 5, and 7, the GCD is 1 (as they are all prime and share no common factors other than 1). Therefore:
LCM(2, 5, 7) * GCD(2, 5, 7) = 2 * 5 * 7
LCM(2, 5, 7) * 1 = 70
LCM(2, 5, 7) = 70
Applications of LCM
The LCM has numerous applications in various fields:
-
Scheduling: Imagine you have three tasks that repeat at different intervals: Task A every 2 days, Task B every 5 days, and Task C every 7 days. To find when all three tasks will coincide, you need to find the LCM of 2, 5, and 7, which is 70. This means all three tasks will align every 70 days.
-
Fraction Arithmetic: When adding or subtracting fractions with different denominators, finding the LCM of the denominators helps determine the least common denominator (LCD), simplifying the calculation.
-
Cyclic Processes: In physics and engineering, many processes are cyclical. Finding the LCM helps determine when cycles will align or repeat simultaneously.
-
Music Theory: LCM is used to determine the least common multiple of the note durations to determine the length of a musical phrase.
-
Computer Science: In areas like scheduling processes or managing concurrent tasks in operating systems, LCM plays a critical role in optimizing resource allocation and performance.
Further Exploration: LCM of Larger Numbers
The methods described above are applicable to any number of integers. For larger numbers, the prime factorization method often proves to be the most efficient. However, for exceptionally large numbers, specialized algorithms are employed to optimize the calculation.
For example, let's find the LCM of 12, 18, and 30:
- Prime factorization of 12: 2² * 3¹
- Prime factorization of 18: 2¹ * 3²
- Prime factorization of 30: 2¹ * 3¹ * 5¹
The LCM will be 2² * 3² * 5¹ = 4 * 9 * 5 = 180
Therefore, the LCM of 12, 18, and 30 is 180.
Conclusion: Mastering LCM Calculations
Understanding the concept of the least common multiple and mastering different methods for calculating it is crucial for various mathematical applications. Whether using the listing multiples method for small numbers or the more efficient prime factorization method for larger numbers, the ability to calculate the LCM empowers you to solve problems in diverse fields. The applications of LCM extend far beyond basic arithmetic, making it a valuable tool in various disciplines. This comprehensive guide provides you with the knowledge and techniques to confidently tackle LCM problems, solidifying your understanding of this fundamental mathematical concept.
Latest Posts
Latest Posts
-
How Do You Find The Inverse Of A Relation
Mar 17, 2025
-
Does Cold Air Go Up Or Down
Mar 17, 2025
-
Least Common Multiple Of 20 And 3
Mar 17, 2025
-
Function Of The Motor End Plate
Mar 17, 2025
-
A Push Or A Pull Is Called
Mar 17, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 5 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
