Is Square Root Of 15 A Rational Number
Juapaving
Mar 26, 2025 · 4 min read
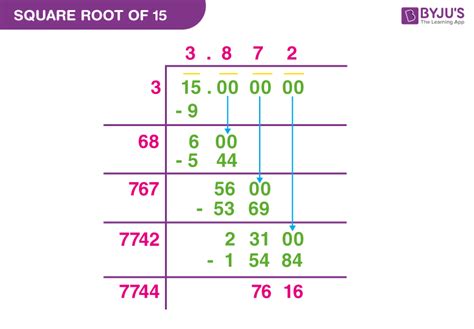
Table of Contents
Is the Square Root of 15 a Rational Number? A Deep Dive into Irrationality
The question of whether the square root of 15 is a rational number is a fundamental concept in mathematics, touching upon the core distinctions between rational and irrational numbers. Understanding this requires a grasp of what constitutes a rational number and the properties of square roots. This article will not only answer the question definitively but also explore the underlying mathematical principles and provide a robust understanding of irrational numbers.
What are Rational Numbers?
A rational number is any number that can be expressed as the quotient or fraction p/q of two integers, a numerator 'p', and a non-zero denominator 'q'. Crucially, this fraction must be able to be simplified to a finite decimal or a repeating decimal. Examples include:
- 1/2 (0.5)
- 3/4 (0.75)
- 2/3 (0.666...)
- -5/7 (-0.714285714285...)
The key here is the ability to represent the number as a ratio of two integers.
What are Irrational Numbers?
Irrational numbers, on the other hand, cannot be expressed as a simple fraction of two integers. Their decimal representation is neither terminating nor repeating. Famous examples include:
- π (pi): Approximately 3.14159..., its digits continue infinitely without any repeating pattern.
- e (Euler's number): Approximately 2.71828..., also with an infinite, non-repeating decimal expansion.
- √2 (the square root of 2): This is the length of the diagonal of a square with sides of length 1. It cannot be expressed as a fraction of two integers.
The existence of irrational numbers was a significant breakthrough in ancient Greek mathematics, challenging the prevailing belief that all numbers could be represented as ratios.
Proving the Irrationality of √15
To definitively answer whether √15 is rational, we employ a technique called proof by contradiction. This method assumes the opposite of what we want to prove and then demonstrates that this assumption leads to a logical contradiction, thus proving the original statement.
Let's assume, for the sake of contradiction, that √15 is a rational number. This means it can be expressed as a fraction p/q, where p and q are integers, q ≠ 0, and the fraction is in its simplest form (meaning p and q share no common factors other than 1).
So, we have:
√15 = p/q
Squaring both sides, we get:
15 = p²/q²
Rearranging the equation:
15q² = p²
This equation tells us that p² is a multiple of 15. Since 15 = 3 x 5, it means p² is divisible by both 3 and 5. If p² is divisible by a prime number, then p itself must also be divisible by that prime number. Therefore, p must be divisible by both 3 and 5. We can express this as:
p = 3 * 5 * k = 15k, where k is an integer.
Substituting this back into the equation 15q² = p², we get:
15q² = (15k)²
15q² = 225k²
Dividing both sides by 15:
q² = 15k²
This equation shows that q² is also a multiple of 15, and therefore q is divisible by both 3 and 5.
Here's the contradiction: We initially assumed that p/q is in its simplest form, meaning p and q share no common factors. However, we've just shown that both p and q are divisible by 15, contradicting our initial assumption.
Therefore, our initial assumption that √15 is rational must be false.
Conclusion: √15 is an irrational number.
Understanding the Implications of Irrationality
The irrationality of √15 has several important implications:
-
Infinite Non-Repeating Decimal: The decimal representation of √15 is infinite and does not repeat. While we can approximate it (approximately 3.87298), we can never express it exactly as a finite or repeating decimal.
-
Geometric Significance: The irrationality of √15 relates to geometric constructions. For instance, it's impossible to construct a line segment of length √15 using only a compass and straightedge.
-
Number System Completeness: The existence of irrational numbers completes the number system, highlighting the richness and complexity of mathematical concepts.
Exploring Similar Irrational Numbers
The proof method used for √15 can be adapted to prove the irrationality of many other square roots of non-perfect squares. For example, √2, √3, √7, √11, and countless others are all irrational. The key is that the number under the square root doesn't have perfect square factors other than 1.
Practical Applications and Further Exploration
While the concept of irrationality might seem purely theoretical, it has practical applications in various fields:
-
Physics: Irrational numbers frequently appear in physical phenomena, such as the calculations involving pi in circular motion or the golden ratio in natural patterns.
-
Engineering: Precise calculations in engineering often involve irrational numbers, necessitating the use of approximations and careful consideration of error margins.
-
Computer Science: The representation and handling of irrational numbers in computer systems require sophisticated algorithms and data structures.
Conclusion: A Solid Foundation in Number Theory
Understanding the nature of rational and irrational numbers, and specifically why √15 is irrational, forms a cornerstone of mathematical understanding. The proof by contradiction method employed in this analysis is a powerful tool in mathematics, demonstrating the elegance and rigor of mathematical reasoning. Further exploring the intricacies of number theory opens up a world of fascinating mathematical concepts and applications. Remember, the journey of mathematical discovery is a continuous process of questioning, exploring, and refining our understanding of the fundamental building blocks of numbers.
Latest Posts
Latest Posts
-
Give The Temperature And Pressure At Stp
Mar 29, 2025
-
Give The Ground State Electron Configuration For Pb
Mar 29, 2025
-
Worksheet On Simple Compound And Complex Sentences With Answers
Mar 29, 2025
-
Lowest Common Multiple Of 6 8 And 9
Mar 29, 2025
-
Is A Amino Acid A Carbohydrate
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Is Square Root Of 15 A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
