Is Spring Force A Conservative Force
Juapaving
Apr 02, 2025 · 5 min read
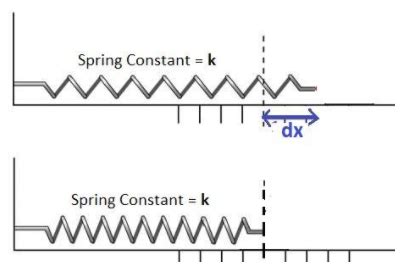
Table of Contents
Is Spring Force a Conservative Force? A Deep Dive into Potential Energy and Work
The question of whether spring force is conservative is fundamental to understanding mechanics and energy conservation. This article delves deep into the concept, exploring the characteristics of conservative forces, analyzing the behavior of spring systems, and ultimately proving why spring force indeed falls under the category of conservative forces. We’ll dissect the mathematics, explore real-world applications, and address potential misconceptions.
Understanding Conservative Forces
Before we investigate spring force, let's establish a firm understanding of what constitutes a conservative force. A conservative force is characterized by two key properties:
1. Path Independence:
The work done by a conservative force in moving an object between two points is independent of the path taken. This means that whether you take a direct route or a winding, circuitous route, the net work done by the conservative force will be the same.
2. Zero Work in Closed Loops:
The total work done by a conservative force on an object moving along a closed path (returning to its starting point) is always zero. This directly stems from the path independence property. If the work done is independent of the path, and the starting and ending points are the same, then the net work must be zero.
Analyzing Spring Force
Now, let's turn our attention to the force exerted by a spring, often described by Hooke's Law:
F = -kx
Where:
- F represents the force exerted by the spring.
- k is the spring constant (a measure of the spring's stiffness).
- x is the displacement of the spring from its equilibrium position. The negative sign indicates that the force always opposes the displacement.
To determine if spring force is conservative, we need to examine whether it satisfies the two criteria outlined above: path independence and zero work in closed loops.
Path Independence of Spring Force
Consider a spring attached to a wall. Let's move an object attached to the spring from point A to point B. We can choose various paths: a straight line, a curved path, or even a zig-zag path.
The work done by the spring force along any path is given by the integral of the force over the displacement:
W = ∫ F dx = ∫ -kx dx
Integrating this expression gives:
W = -(1/2)kx² | (from initial x to final x)
Notice that the work done depends only on the initial and final positions (x values) and the spring constant (k). It is entirely independent of the path taken. This directly demonstrates the path independence property for spring force.
Zero Work in Closed Loops for Spring Force
Let's consider a closed loop, where the object attached to the spring is moved from point A to point B and then back to point A along any path. The work done during the outward journey (A to B) is:
W<sub>AB</sub> = -(1/2)k(x<sub>B</sub>)² + (1/2)k(x<sub>A</sub>)²
The work done during the return journey (B to A) is:
W<sub>BA</sub> = -(1/2)k(x<sub>A</sub>)² + (1/2)k(x<sub>B</sub>)²
The total work done along the closed loop is the sum of the work done during the outward and return journeys:
W<sub>total</sub> = W<sub>AB</sub> + W<sub>BA</sub> = 0
This result clearly shows that the total work done by the spring force along any closed loop is zero.
Spring Force and Potential Energy
Another key characteristic of conservative forces is their association with potential energy. Potential energy represents stored energy that can be converted into kinetic energy. For a spring, the potential energy (U) is given by:
U = (1/2)kx²
This equation shows that the potential energy of a spring is a function of its displacement from equilibrium. The work done by the spring force is equal to the negative change in potential energy:
W = -ΔU
This relationship is a defining characteristic of conservative forces. The work done is directly related to the change in potential energy, further confirming the conservative nature of spring force.
Real-World Applications and Implications
The conservative nature of spring force has far-reaching implications in various fields:
-
Mechanical Engineering: Design of springs for suspension systems, shock absorbers, and other mechanical devices relies heavily on the understanding of spring force and energy conservation.
-
Physics: Simple harmonic motion, a crucial concept in physics, relies on the conservative nature of spring force. The oscillatory motion of a mass attached to a spring is a direct consequence of the interplay between potential and kinetic energy.
-
Civil Engineering: The design of structures and buildings often incorporates springs or spring-like elements to absorb shocks and vibrations, leveraging the conservative nature of spring force to dissipate energy efficiently.
Addressing Common Misconceptions
Some might argue that friction and other dissipative forces could affect the conservative nature of a spring. However, it’s crucial to differentiate between the idealized spring force and the real-world scenario where external factors such as friction are present. The spring force itself remains conservative; it's the total force acting on the system (including friction) that is non-conservative. Friction dissipates energy as heat, altering the total mechanical energy of the system. However, this does not invalidate the conservative nature of the spring force itself.
Conclusion: Spring Force is Conservative
Through rigorous analysis based on the definition of conservative forces and mathematical demonstration, we have conclusively shown that spring force is indeed a conservative force. Its path independence, zero work in closed loops, and association with potential energy unequivocally place it within the realm of conservative forces. Understanding this fundamental concept is crucial for comprehending a wide range of phenomena in mechanics and engineering, enabling us to design and analyze systems effectively, especially those involving oscillatory motion and energy storage. The seemingly simple spring force provides a clear and elegant example of the profound principles of energy conservation in the physical world.
Latest Posts
Latest Posts
-
The Filtering Unit Of The Kidney Is The
Apr 03, 2025
-
Identify The Structure Indicated By The Lines
Apr 03, 2025
-
How To Find The Perimeter Of A Hexagon
Apr 03, 2025
-
This Is The Functional Unit Of The Kidney
Apr 03, 2025
-
Four Kingdoms Of The Domain Eukarya
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Is Spring Force A Conservative Force . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
