Is Area The Same As Surface Area
Juapaving
Mar 29, 2025 · 6 min read
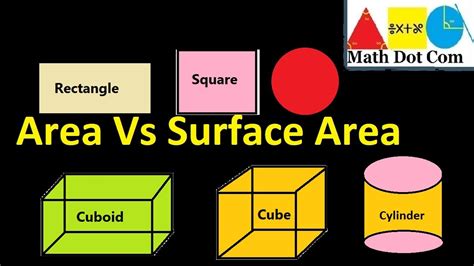
Table of Contents
Is Area the Same as Surface Area? A Deep Dive into Geometric Measurement
The terms "area" and "surface area" are often used interchangeably, leading to confusion, especially in geometry and related fields. While seemingly similar, they represent distinct concepts with specific applications. This comprehensive guide will delve into the precise definitions of area and surface area, highlight their key differences, and explore various examples to solidify your understanding. We'll also examine how these concepts are used in different contexts and discuss potential pitfalls to avoid.
Understanding Area: A Two-Dimensional Measurement
Area, in its simplest form, refers to the two-dimensional space occupied by a flat shape or figure. It quantifies the amount of surface enclosed within a given boundary. Think of it as the amount of paint needed to cover a flat surface completely. The units used to measure area are always squared units, such as square meters (m²), square centimeters (cm²), square feet (ft²), or square inches (in²).
Calculating Area for Common Shapes:
The methods for calculating area vary depending on the shape:
- Rectangle: Area = length × width
- Square: Area = side × side (or side²)
- Triangle: Area = ½ × base × height
- Circle: Area = π × radius²
- Parallelogram: Area = base × height
- Trapezoid: Area = ½ × (base1 + base2) × height
These formulas provide a straightforward way to determine the area of basic geometric shapes. More complex shapes often require breaking them down into simpler components or using integral calculus.
Applications of Area Measurement:
Area calculations are essential in a wide range of fields:
- Construction and Engineering: Determining material quantities (e.g., flooring, roofing), land surveying, and structural design.
- Agriculture: Calculating land acreage for planting and yield estimation.
- Cartography: Representing geographical areas on maps.
- Real Estate: Determining property sizes and values.
- Interior Design: Planning room layouts and material requirements.
- Computer Graphics: Representing and manipulating two-dimensional objects.
Unveiling Surface Area: A Three-Dimensional Perspective
Surface area, unlike area, is a three-dimensional concept. It refers to the total area of all the external surfaces of a three-dimensional object. Imagine wrapping a present – the surface area is the total area of the wrapping paper required to cover the gift completely, without any overlaps or gaps. The units used to measure surface area are also squared units, consistent with area measurements.
Calculating Surface Area for Common 3D Shapes:
The calculation of surface area depends heavily on the object's shape:
- Cube: Surface Area = 6 × side² (since a cube has 6 identical square faces)
- Cuboid (rectangular prism): Surface Area = 2 × (length × width + length × height + width × height)
- Sphere: Surface Area = 4 × π × radius²
- Cylinder: Surface Area = 2 × π × radius × height + 2 × π × radius² (lateral surface area + area of the two circular bases)
- Cone: Surface Area = π × radius × slant height + π × radius² (lateral surface area + area of the circular base)
- Pyramid: Surface Area depends on the shape of the base and the number of triangular faces. Each face needs to be calculated individually and then summed.
Calculating surface area for more complex 3D objects often involves calculus and more sophisticated mathematical techniques. Approximation methods can be used for irregular shapes.
Practical Applications of Surface Area:
Understanding surface area is crucial in various disciplines:
- Packaging and Manufacturing: Determining the amount of material needed for packaging products efficiently.
- Heat Transfer: Calculating the rate of heat loss or gain from an object based on its surface area.
- Fluid Dynamics: Analyzing the interaction between fluids and solid surfaces.
- Biology: Studying the surface area-to-volume ratio of cells and organisms, influencing efficiency of nutrient uptake and waste removal.
- Environmental Science: Calculating the surface area of pollutants in the environment to estimate the extent of contamination.
- Medical Science: Determining the surface area of wounds for treatment planning.
Key Differences between Area and Surface Area:
The fundamental difference lies in the dimensionality of the measurement:
| Feature | Area | Surface Area |
|---|---|---|
| Dimensionality | Two-dimensional (2D) | Three-dimensional (3D) |
| Object Type | Flat shapes (e.g., squares, circles) | Three-dimensional objects (e.g., cubes, spheres) |
| Measurement | Amount of space enclosed within a boundary | Total area of all external surfaces |
| Units | Square units (m², cm², ft², in²) | Square units (m², cm², ft², in²) |
| Calculation | Relatively straightforward for regular shapes | Can be complex, especially for irregular shapes |
Common Misconceptions and Pitfalls:
-
Interchangeable Use: The most common mistake is using "area" and "surface area" interchangeably. Remember that area applies only to two-dimensional figures, while surface area deals with three-dimensional objects.
-
Confusing Volume with Surface Area: Volume measures the three-dimensional space inside an object, while surface area measures the external surfaces. They are distinct concepts.
-
Ignoring Complex Shapes: Calculating surface area for complex shapes can be challenging and often requires advanced mathematical techniques or approximation methods. Care must be taken to avoid errors in segmentation and calculations.
-
Unit Inconsistencies: Always ensure consistent units throughout the calculation. Mixing units (e.g., centimeters and meters) will lead to incorrect results.
Real-World Examples to Illustrate the Difference:
Consider a rectangular box (cuboid):
-
Area: You might calculate the area of one of its faces (length x width) to determine the amount of material needed for a label. This is a two-dimensional measurement related to a single face.
-
Surface Area: To calculate the total amount of cardboard required to construct the box, you would determine its surface area. This involves summing the area of all six faces of the box. This is a three-dimensional measurement encompassing the entire external surface.
Similarly, consider a circular pizza:
-
Area: The area of the pizza represents the amount of edible surface. This is a two-dimensional calculation.
-
Surface Area: While not commonly used in this context, the surface area would consider both the top and bottom surfaces of the pizza, if you were trying to calculate how much greaseproof paper is needed to cover both sides.
Conclusion: A Clear Distinction is Crucial
The distinction between area and surface area is essential for accurate measurements and calculations in various applications. While they both use squared units, area focuses on two-dimensional shapes, whereas surface area deals with the total external area of three-dimensional objects. Understanding their differences, along with the methods for calculating each, is crucial for anyone working with geometric concepts, whether in academic settings, professional fields, or everyday life. Avoiding the common pitfalls and remembering the distinct applications of each term ensures accuracy and comprehension in geometrical measurement.
Latest Posts
Latest Posts
-
What Is 3 33333 As A Fraction
Apr 01, 2025
-
What Does A Prokaryotic Cell Not Have
Apr 01, 2025
-
What Are More Things About The Major Components Of Soil
Apr 01, 2025
-
What Is The Lcm Of 5 6 7
Apr 01, 2025
-
Find The Complementary And Supplementary Angles
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Is Area The Same As Surface Area . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
