Is 2 6 Greater Than 1 3
Juapaving
May 13, 2025 · 5 min read
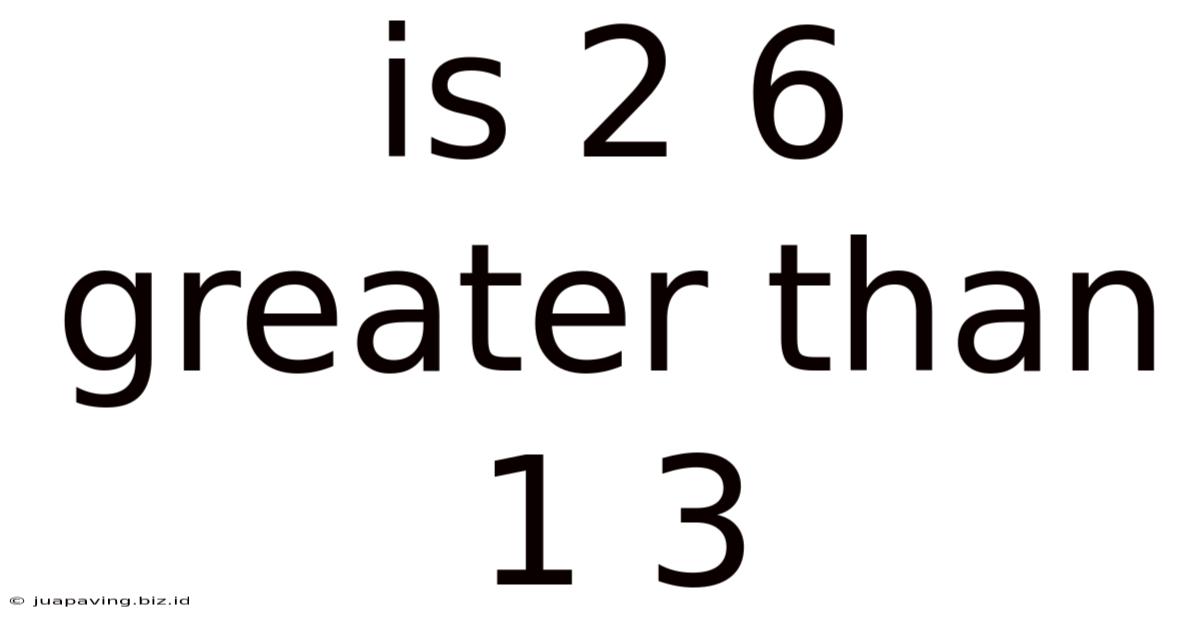
Table of Contents
Is 2/6 Greater Than 1/3? A Deep Dive into Fraction Comparison
The question, "Is 2/6 greater than 1/3?", might seem simple at first glance. For those comfortable with fractions, the answer is readily apparent. However, understanding why one fraction is larger or smaller than another is crucial for developing a solid foundation in mathematics. This article will not only answer the question definitively but also explore various methods for comparing fractions, highlighting the importance of equivalent fractions and simplifying expressions. We'll even delve into the practical applications of fraction comparison in everyday life.
Understanding Fractions: A Quick Refresher
Before we tackle the core question, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number represents the number of parts we have.
- Denominator: The bottom number represents the total number of equal parts the whole is divided into.
For example, in the fraction 2/6, 2 is the numerator (we have 2 parts), and 6 is the denominator (the whole is divided into 6 equal parts). Similarly, in 1/3, 1 is the numerator, and 3 is the denominator.
Method 1: Simplifying Fractions
One of the most effective ways to compare fractions is to simplify them to their lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
Let's simplify 2/6:
The GCD of 2 and 6 is 2. Dividing both the numerator and denominator by 2, we get:
2/6 = (2 ÷ 2) / (6 ÷ 2) = 1/3
Now we can directly compare 1/3 and 1/3. They are equal. Therefore, 2/6 is not greater than 1/3; they are equivalent fractions.
Method 2: Finding a Common Denominator
Another powerful method for comparing fractions is to find a common denominator. This involves converting the fractions so they both have the same denominator. Then, we can simply compare the numerators.
Let's compare 2/6 and 1/3 using this method:
The least common multiple (LCM) of 6 and 3 is 6. We need to convert 1/3 to an equivalent fraction with a denominator of 6. To do this, we multiply both the numerator and denominator by 2:
1/3 = (1 × 2) / (3 × 2) = 2/6
Now we can compare 2/6 and 2/6. Again, we see that they are equal.
Method 3: Visual Representation
Visual aids can be incredibly helpful, especially when working with fractions. Imagine a circle divided into six equal parts. Shading two of those parts represents the fraction 2/6. Now, imagine another circle divided into three equal parts. Shading one of those parts represents the fraction 1/3. Visually, you can see that both shaded areas are the same size, confirming that 2/6 and 1/3 are equivalent.
Why Understanding Fraction Comparison Matters
The ability to compare fractions is fundamental to many mathematical concepts and real-world applications. It's essential for:
- Solving equations: Many algebraic equations involve fractions, and comparing them is often necessary to find solutions.
- Understanding proportions: Proportions are crucial in various fields, from cooking and construction to finance and science. Comparing fractions helps determine ratios and proportions.
- Data analysis: When working with data represented as fractions (e.g., percentages, parts of a whole), comparing fractions is crucial for drawing accurate conclusions.
- Everyday tasks: From dividing recipes to measuring ingredients, understanding fractions is a valuable life skill.
Beyond the Basics: Exploring More Complex Fraction Comparisons
While the comparison of 2/6 and 1/3 is relatively straightforward, more complex scenarios might involve comparing fractions with different denominators and numerators that aren't easily simplified. In these cases, the methods outlined above—finding a common denominator or simplifying fractions—remain essential tools.
Example: Comparing 5/8 and 3/5
Let's compare 5/8 and 3/5. Neither fraction simplifies further. To compare them, we'll find a common denominator:
The LCM of 8 and 5 is 40. We convert both fractions to equivalent fractions with a denominator of 40:
5/8 = (5 × 5) / (8 × 5) = 25/40 3/5 = (3 × 8) / (5 × 8) = 24/40
Now, comparing the numerators, we see that 25/40 > 24/40, therefore 5/8 > 3/5.
Decimal Equivalents: Another Approach
Another way to compare fractions is to convert them into decimal equivalents. This involves dividing the numerator by the denominator.
For example:
2/6 = 0.333... 1/3 = 0.333...
Again, we see that their decimal equivalents are equal, confirming that 2/6 = 1/3.
This method is particularly useful when dealing with fractions that are difficult to simplify or find a common denominator for. However, remember that recurring decimals might require rounding, which can introduce a small margin of error.
Conclusion: Mastering Fraction Comparison
The comparison of fractions, while seemingly basic, is a foundational mathematical skill with far-reaching applications. Understanding the various methods for comparing fractions—simplifying, finding common denominators, visual representation, and using decimal equivalents—is crucial for success in mathematics and in numerous real-world situations. The question, "Is 2/6 greater than 1/3?", serves as a perfect springboard to explore these essential concepts and develop a deeper understanding of fractions. By mastering these techniques, you'll equip yourself with a powerful tool for solving problems and navigating mathematical challenges with confidence. Remember to always simplify your fractions whenever possible to make comparisons easier and more efficient. Practice regularly, and you'll find yourself effortlessly comparing fractions of any complexity.
Latest Posts
Latest Posts
-
What Color Is A Plant Cell
May 13, 2025
-
An Alloy Of Copper And Tin
May 13, 2025
-
Greatest Common Factor Of 9 And 7
May 13, 2025
-
5 Letter Word Beginning With A And Ending With T
May 13, 2025
-
What Is A Quarter Past 12
May 13, 2025
Related Post
Thank you for visiting our website which covers about Is 2 6 Greater Than 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.