In An Exponential Function What Does The A Represent
Juapaving
Apr 01, 2025 · 6 min read
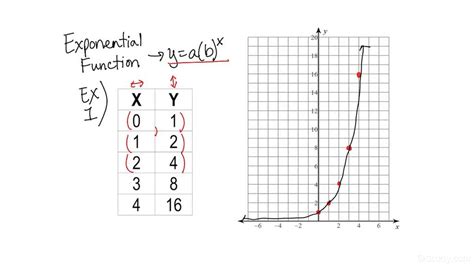
Table of Contents
In an Exponential Function, What Does 'a' Represent? A Deep Dive
The exponential function, a cornerstone of mathematics and crucial across numerous scientific disciplines, often appears in the form y = abˣ. Understanding each component is key to mastering its applications. While 'b' (the base) and 'x' (the exponent) are frequently discussed, the role of 'a' – the initial value or y-intercept – sometimes gets overlooked. This comprehensive guide delves into the significance of 'a' in exponential functions, exploring its impact on graphs, real-world applications, and its relationship with other parameters.
Understanding the Structure: y = abˣ
Before we dive into the intricacies of 'a', let's briefly review the overall structure of the exponential function: y = abˣ.
- y: Represents the dependent variable – the output of the function. Its value depends on the input, x.
- a: This is the initial value, or y-intercept. It represents the value of y when x = 0. We'll explore this in much greater detail below.
- b: The base. This is a constant value that determines the rate of growth or decay. If b > 1, the function represents exponential growth. If 0 < b < 1, it represents exponential decay.
- x: The independent variable, or input. It often represents time, but can be any other relevant variable depending on the context.
The Significance of 'a': The Initial Value and its Impact
The parameter 'a' in the exponential function y = abˣ serves as the initial value or the y-intercept. This means it's the value of the dependent variable (y) when the independent variable (x) is equal to zero. Think of it as the starting point of the exponential growth or decay process.
Geometrically: On a graph representing the exponential function, 'a' determines where the curve intersects the y-axis. If a = 1, the curve passes through the point (0, 1). If a = 2, it passes through (0, 2), and so on. A positive 'a' indicates the curve starts above the x-axis, while a negative 'a' reflects the curve starting below the x-axis. This is assuming a positive value of 'b'.
Numerically: If you substitute x = 0 into the equation y = abˣ, you get y = a(b⁰) = a(1) = a. This clearly demonstrates that 'a' directly corresponds to the y-intercept.
Transformations with 'a'
Altering the value of 'a' directly influences the vertical scaling of the graph. Multiplying 'a' by a constant (k) stretches or compresses the graph vertically.
- k > 1: Vertical stretch – The graph gets taller.
- 0 < k < 1: Vertical compression – The graph gets shorter.
- k < 0: The graph is reflected across the x-axis and stretches/compresses vertically based on the absolute value of k.
For example, compare y = 2(3ˣ) and y = 4(3ˣ). The second function has double the initial value and will result in a graph that is twice as tall at any given x value.
Real-World Applications: 'a' in Context
The significance of 'a' becomes clearer when we examine real-world applications of exponential functions:
1. Population Growth: Consider modeling a population's growth over time. The exponential function P(t) = abᵗ could represent the population (P) at time t, where:
- a: Represents the initial population size (the population at time t = 0).
- b: Represents the growth factor (1 + growth rate).
- t: Represents time (often in years).
The value of 'a' directly influences the initial population which, in turn, impacts the growth curve over time. A larger 'a' leads to a steeper curve than a smaller 'a', assuming all other factors remain constant.
2. Radioactive Decay: Radioactive decay follows an exponential decay model. The equation for the remaining amount (A) of a radioactive substance after time (t) is often given by:
A(t) = a(1/2)^(t/h)
Where:
- a: Represents the initial amount of the radioactive substance.
- 1/2: Represents the decay factor (half-life).
- h: Represents the half-life period.
- t: Represents time.
'a' in this case signifies the original amount of the substance. It determines the starting point of the decay process.
3. Compound Interest: The classic formula for compound interest is another clear example where 'a' plays a critical role.
A = P(1 + r/n)^(nt)
Where:
- A: Final amount
- P: Principal amount (initial investment): This is the 'a' in our exponential function analogy.
- r: Annual interest rate (decimal)
- n: Number of times that interest is compounded per year
- t: Number of years
Here, 'a' is the principal amount – the initial investment. It forms the foundation upon which the interest compounds over time.
'a' and Other Exponential Function Parameters: Interactions
The value of 'a' doesn't exist in isolation. Its interplay with the base ('b') significantly impacts the overall behavior of the exponential function.
Interaction with the Base (b)
While 'b' dictates the rate of growth or decay, 'a' sets the scale. A larger 'a' simply stretches the graph vertically; the rate of growth or decay remains determined by 'b'. Both work together to produce the final shape and position of the curve. For instance, comparing y = 2(1.5ˣ) and y = 2(2ˣ) shows that even though both start at the same value of 'a'=2, the function with b=2 grows much faster than the function with b=1.5.
Horizontal Asymptotes and 'a'
In exponential functions where 0 < b < 1 (decay), there's a horizontal asymptote at y = 0. The value of 'a' doesn't alter the location of this asymptote, but it determines how quickly the function approaches it. A larger 'a' means the curve approaches the asymptote from a higher position.
Advanced Concepts: Exponential Functions with More Complex Forms
The basic form y = abˣ can be extended to incorporate additional parameters, such as horizontal and vertical shifts:
- y = a * b^(x-h) + k
Here:
- h: Represents a horizontal shift (moving the graph left or right).
- k: Represents a vertical shift (moving the graph up or down).
In this more general form, 'a' still maintains its role as the initial value, but this value is after any horizontal shifts and before any vertical shifts are applied. The effect of a horizontal shift, h, will directly influence what value of x results in y=a. In essence, it determines the y-value when x=h. A vertical shift, k, however, adds to the initial value of a, influencing the entire function by shifting it upwards or downwards.
Conclusion: Mastering the 'a' in Exponential Functions
Understanding the role of 'a' in exponential functions is crucial for interpreting and applying these fundamental mathematical models. Whether it represents an initial population size, an initial amount of a radioactive substance, or a principal investment, 'a' establishes the starting point of the exponential growth or decay process. It works in conjunction with the base ('b') to determine the overall shape, scale, and position of the exponential curve, impacting numerous applications across diverse scientific and financial fields. By grasping this vital component, you enhance your understanding and ability to use exponential functions effectively and accurately.
Latest Posts
Latest Posts
-
Cervical Thoracic And Lumbar Vertebrae Differences
Apr 02, 2025
-
Are All Cells The Same Shape And Size
Apr 02, 2025
-
What Are Rows Called In The Periodic Table
Apr 02, 2025
-
120 Mins Is How Many Hours
Apr 02, 2025
-
How Many Miles Are In 10 Kilometers
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about In An Exponential Function What Does The A Represent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
