How To Prove That Parallel Lines Mean Equal Alternate Angles
Juapaving
Mar 27, 2025 · 5 min read
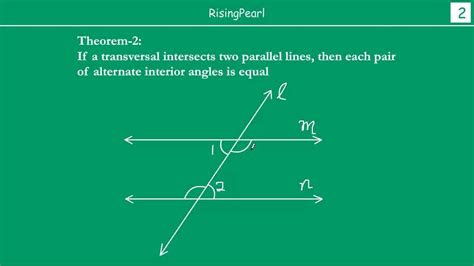
Table of Contents
How to Prove That Parallel Lines Mean Equal Alternate Angles
This article provides a comprehensive exploration of how to prove the theorem stating that when a transversal intersects two parallel lines, the alternate interior angles are equal. We'll delve into various approaches to this proof, including using axiomatic geometry, transformations, and even exploring the intuitive understanding behind the concept. This exploration aims to provide a robust understanding suitable for various levels of mathematical comprehension.
Understanding the Theorem and its Components
Before we dive into the proofs, let's define the key terms:
-
Parallel Lines: Two lines that never intersect, regardless of how far they are extended. They maintain a constant distance from each other.
-
Transversal Line: A line that intersects two or more other lines at distinct points.
-
Alternate Interior Angles: These are pairs of angles formed when a transversal intersects two lines. They are located inside the two lines and on opposite sides of the transversal.
The theorem we aim to prove states: If two parallel lines are intersected by a transversal, then the alternate interior angles are congruent (equal in measure).
Proof 1: Using Axiomatic Geometry (Euclidean Geometry)
This proof relies on the postulates and theorems of Euclidean geometry. We'll use a common approach that builds upon other established geometric facts.
1. Assumptions:
- We have two parallel lines, l and m.
- A transversal line, t, intersects both l and m.
- We label the alternate interior angles as ∠1 and ∠2.
2. Constructing Auxiliary Lines:
Draw a line n parallel to the transversal t and passing through the intersection point of l and t.
3. Utilizing Properties of Parallel Lines and Transversals:
-
Consecutive Interior Angles are Supplementary: Because l and m are parallel and t is a transversal, consecutive interior angles (like ∠1 and an angle adjacent to ∠2 on line m) are supplementary. Their sum is 180 degrees. This is a theorem established in Euclidean geometry.
-
Vertical Angles are Congruent: The angles formed by the intersection of t and n are vertically opposite angles and therefore congruent.
-
Corresponding Angles are Congruent (when lines are parallel): Since n is parallel to t, and l is a transversal, corresponding angles are equal.
4. Deduction:
By combining these established properties, we can show that ∠1 and ∠2 are equal. The specific steps may vary slightly depending on the exact layout of the diagram and the order in which theorems are applied, but the essence is to use supplementary angles and vertical angles to connect ∠1 and ∠2. Since consecutive interior angles add to 180°, and vertical angles are equal, we can prove that the alternate interior angles ∠1 and ∠2 are also equal.
5. Conclusion:
Therefore, we have proven that if two parallel lines are intersected by a transversal, then the alternate interior angles are congruent.
Proof 2: Using Transformations (Isometries)
This approach utilizes the concept of transformations in geometry, specifically translations.
1. Assumptions: Same as Proof 1.
2. Translation:
Imagine translating line l along the transversal t until it coincides with line m. This is a rigid transformation (an isometry) that preserves angles and distances.
3. Observation:
After the translation, ∠1 will perfectly overlap ∠2. This is because the translation moves l parallel to itself, maintaining its orientation relative to t.
4. Conclusion:
Since ∠1 and ∠2 perfectly overlap after the translation, they must be congruent (equal). This proves the theorem. This method offers a more visual and intuitive grasp of the proof.
Proof 3: Intuitive Understanding and Real-World Examples
While formal proofs are essential, understanding the intuition behind the theorem strengthens comprehension.
Imagine laying two parallel rulers on a flat surface. The transversal would be a straight edge placed across them. No matter where you place the transversal, the angles on opposite sides of the transversal will always match. This visual representation helps solidify the idea that parallel lines necessitate equal alternate interior angles.
Consider railroad tracks. The tracks are parallel lines, and a crosswalk (transversal) will form angles. Observe how the alternate interior angles are always equal.
Converse of the Theorem: Equal Alternate Interior Angles Imply Parallel Lines
It's crucial to understand the converse of this theorem: If two lines are intersected by a transversal, and the alternate interior angles are congruent, then the lines are parallel. This is equally important and can be proven using proof by contradiction or similar geometric techniques, showing that if the lines were not parallel, the alternate interior angles couldn't be equal.
Applications of the Theorem
This theorem is fundamental to numerous areas of mathematics and related fields:
-
Geometry: It's essential for solving geometric problems involving parallel lines and transversals, determining unknown angles, and proving other geometric theorems.
-
Trigonometry: The relationships between angles are crucial in solving trigonometric problems.
-
Engineering and Architecture: Parallel lines and angles are critical in construction, structural design, and surveying to ensure accuracy and stability.
-
Computer Graphics: Understanding these relationships is vital in creating accurate and realistic representations of objects in computer graphics.
Advanced Considerations and Extensions
-
Non-Euclidean Geometries: In non-Euclidean geometries (like spherical or hyperbolic geometry), this theorem doesn't necessarily hold true. The nature of parallel lines differs significantly in these systems.
-
Projective Geometry: Projective geometry offers alternative perspectives on parallel lines and their intersections at infinity.
-
Vector Geometry: Vector methods provide alternative proofs using vector operations and dot products.
Conclusion
Proving that parallel lines imply equal alternate interior angles is a foundational concept in geometry. This article explored multiple approaches, from rigorous axiomatic proofs to more intuitive visual explanations, aiming to provide a deep understanding of this important theorem. Its applications extend far beyond theoretical mathematics, demonstrating its practicality across numerous scientific and engineering fields. Mastering this concept is key to further explorations in geometry and related disciplines.
Latest Posts
Latest Posts
-
Write 72 As A Product Of Prime Factors
Mar 30, 2025
-
How To Find The Latus Rectum Of A Parabola
Mar 30, 2025
-
Greatest Common Factor Of 24 And 30
Mar 30, 2025
-
What Are All Of The Factors Of 49
Mar 30, 2025
-
Lowest Common Factor Of 3 And 8
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about How To Prove That Parallel Lines Mean Equal Alternate Angles . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
